Вариант 18

Дядя Ваня является постоянным покупателем магазина электрооборудования. Он решил по программе лояльности купить там автомойку, цена которой 5600 рублей. После совершения покупки, 2 % стоимости которой он оплатил бонусами, ему начислили ещё 56 бонусов. Сколько бонусов стало у дяди Вани, если до покупки у него было 245 бонусов? (1 бонус = 1 рубль)

На графике отмечено количество математических задач, решённых каждой из трех подружек: Аней, Светой и Олей. Они решали задачи с понедельника по пятницу.

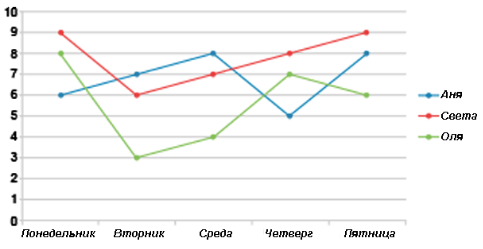
По графику определите, сколько дней количество задач, решённых Олей, было меньше, чем у других девочек.

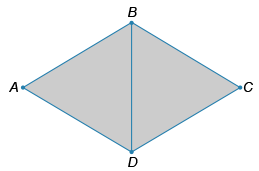
Найдите периметр ромба ABCD, если периметр треугольника ABD равен 36 см, а угол DAB равен 60°. Ответ запишите в сантиметрах.

Аттестационный экзамен в автошколе состоит из двух этапов: теории и практики. Вероятность сдать теорию равна 0,8, а вероятность сдать практику равна 0,65. Найдите вероятность сдать аттестационный экзамен в автошколе.

Найдите наименьший корень уравнения [math]\sqrt{x^2-4x+4}=2[/math]

Найдите угол BAC треугольника ABC, если известны координаты его вершин: A(3; 3), B(3; 9), C(6; 6). Ответ запишите в градусах.

Определите количество точек экстремума функции [math]y=3x^4-8x^3[/math]

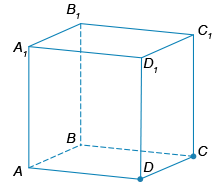
Найдите площадь полной поверхности куба ABCDA1B1C1D1, если A (0; 0,5; 1), B (0; -1; 1).

Найдите значение выражения [math](log_65)(log_54+log_59)[/math]

Радиус окружности, вписанной в прямоугольный треугольник, можно найти по формуле [math]r=\frac{ab}{a+b+\sqrt{a^2+b^2}}[/math], где a и b катеты прямоугольного треугольника. Чему равна длина гипотенузы c (в см), если радиус окружности, вписанной в этот прямоугольный треугольник, равен 1 см, а один из катетов равен 4 см?

Сельский житель Андрей Иванович может убрать свой урожай картофеля за 3 часа, если будет работать один, а если ему будут помогать двое его сыновей, то они вместе смогут убрать этот урожай за 2 часа. За какое время (в часах) уберут весь урожай два сына Андрея Ивановича и соседский мальчишка, если производительность всех трёх ребят одинакова?

Найдите минимум функции [math]y=\frac{x^2+3}{\sqrt x}[/math]

Дано уравнение [math]2\cos x-3\sqrt{2\cos x}+2=0[/math].

а) Решите уравнение.

б) Укажите корни этого уравнения, принадлежащие промежутку [math]\left[-\frac{7\pi}2;\;-2\pi\right][/math].

В правильной треугольной пирамиде SABC сторона основания равна 6, а боковое ребро равно 5. На ребре SC отмечена точка М так, что SM:MС=7:18.

а) Докажите, что плоскости SBC и АВМ перпендикулярны.

б) Найдите объем меньшей части пирамиды SABC, на которые ее разбивает плоскость АВМ.

Решите неравенство [math]\frac{x^2-x+1}{x-1}+\frac{x^2-3x-1}{x-3}\leq2x+2[/math].

В остроугольном треугольнике АВС проведены высоты АК и ВР.

а) Докажите, что углы АКР и АВР равны.

б) Найдите длину отрезка РК, если известно, что АВ=5, ВС=6, СА=4.

1 августа 2016 года Валерий открыл в банке счёт «Пополняй» на четыре года под 10% годовых, вложив 100 тыс. рублей.

1 августа 2017 и 1 августа 2019 года он планирует докладывать на счёт по n тыс. рублей. Найдите наименьшее целое n, при котором к 1 августа 2020 года на счету у Валерия окажется не менее 200 тыс. рублей.

Найдите все а, при каждом из которых уравнение [math]\frac{2a^2-\left(x+3\right)a-x^2+3x}{x^2-9}=0[/math] имеет ровно один корень.

Можно ли n попарно различных натуральных чисел расположить по кругу так, чтобы сумма любых двух соседних чисел являлась точным квадратом, если

а) n = 3;

б) n = 4;

в) n = 5?