Вариант 2
Часть 1.
Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.
Прочитайте внимательно текст и выполните задания 1–5
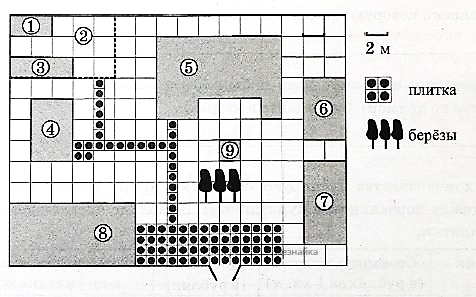
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.
Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.
| Объекты | теплица | коровник | компостная яма | огород | пруд |
| Цифры |
Тротуарная плитка продаётся в упаковках по 5 штук. Сколько упаковок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?
Найдите площадь, которую занимает компостная яма. Ответ дайте в квадратных метрах.
Найдите расстояние от жилого дома до огорода (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.
Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трёх поставщиков плитки.
| Поставщик | Стоимость плитки (в руб. за 1 кв.м.) | Доставка (в руб.) | Работы по демонтажу старой плитки и по укладке новой (в руб.) |
| 1 | 430 | 5000 | 10000 |
| 2 | 425 | 6000 | бесплатно |
| 3 | 500 | бесплатно | 5000 |
Найдите значение выражения
[math](5,5\cdot10^6)\cdot(8\cdot10^{-7})[/math]
Числа a, b, с и d такие, что [math]c<a,d<a,b=d[/math]. Сравните числа b и с.
1) b > c
2) b < c
3) b = c
4) их сравнить невозможно
Значение какого из выражений является рациональным числом?
1) [math]\sqrt7\cdot\sqrt{28}[/math]
2) [math](\sqrt7+1)^2[/math]
3) [math]\sqrt{28}-\sqrt7[/math]
4) [math]\frac{\sqrt7}{28}[/math]
Решите уравнение
[math]\frac3{5x-1}=\frac4{6x}[/math]
На школьной новогодней лотерее будет разыграно 100 подарков. Какова вероятность того, что лотерейный билет выигрышный, если для лотереи было изготовлено и продано 125 билетов?
Установите соответствие между графиком функции и формулой, которая его задает.
A)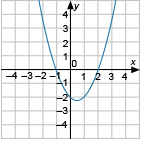 
Б)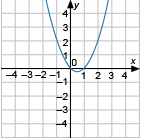 
В)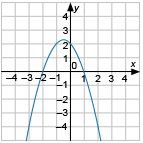 
1) [math]y=x^2-x-2[/math]
2) [math]y=-x^2-x+2[/math]
3) [math]y=x^2-x[/math]
Выпишите цифры, которые соответствуют графикам.
На доске в строку записано 20 чисел так, что каждое последующее число в строке на 11 больше предыдущего. Найдите пятое число, если последнее число равно 250.
Найдите значение выражения
[math]\frac{a-2b}{a^2-4b^2}\cdot\frac{a+2b}{b^2-10a^2}[/math]
при а = [math]\sqrt6[/math], b = 8.
Объём конуса вычисляется по формуле [math]V=\frac{\pi R^2h}3[/math], где r — радиус основания конуса, а h — высота конуса. Пользуясь формулой, найдите радиус основания конуса (в см), если высота конуса равна 6 см, а объём равен 8π см3
Решите систему неравенств: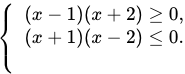 
. Укажите номер правильного ответа.
1) [math](-\infty;-1\rbrack\cup\lbrack1;+\infty)[/math]
2) [math]\lbrack-2;1\rbrack[/math]
3) [math](-\infty;-2\rbrack\cup\lbrack2;+\infty)[/math]
4) [1; 2]
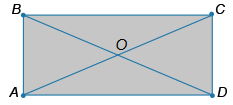
Диагонали прямоугольника ABCD пересекаются в точке O. Найдите длину AO (в см), если стороны прямоугольника равны 5 см и 12 см.
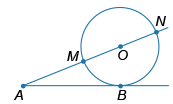
К окружности с центром O проведены касательная AB и секущая AO. Секущая AO пересекает окружность в точках M и N (см. рис.). Найдите длину AB (в см), если AM и AN равны 9 см и 25 см соответственно.
Найдите площадь прямоугольного треугольника ABC, если катеты AC иBC равны 12 см и 8 см соответственно. Ответ дайте в квадратных сантиметрах.
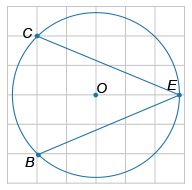
Найдите тангенс угла CEB, изображённого на рисунке.
Укажите номера верных утверждений. Выберите 2 варианта из списка.
1) Существует треугольник со сторонами 5, 8 и 11.
2) Треугольник со сторонами 6, 14 и 17 является прямоугольным.
3) Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе.
4) Диагонали трапеции пересекаются в их общей середине.
Часть 2.
При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Решите неравенство [math]x^2(-x^2-4)\leq4(-x^2-4)[/math]
[math]x^2(-x^2-4)\leq4(-x^2-4)[/math]
(x2-4)(x2+4)≥0
(x2+4)>0 при любом x, так что решим неравенство x2-4≥0
xє(-∞;-2],[2;∞)
Ответ: (-∞;-2],[2;∞)
На строительстве стены первый каменщик работал 5 дней один. Затем к нему присоединился второй, и они вместе закончили работу через 4 дня. Известно, что первому каменщику потребовалось бы на выполнение этой работы на 5 дней больше, чем второму. За сколько дней может выстроить эту стену первый каменщик, работая отдельно?
Пусть Х дней надо первому каменщику на строительство стены. Тогда второму Х-5 дней. Работоспособность первого каменщика 1/Х, а второго - 1/(Х-5), вместе - 1/Х + 1/(Х-5). Проработав 5 дней, первый каменщик закончил работу на 5/Х, затем за 4 дня они вместе сделали 4•(1/Х + 1/(Х-5)), после чего работа была закончена. Составим и решим уравнение.
[math]\frac5x+4\cdot\left(\frac1x+\frac1{x-5}\right)=1[/math]
[math]\frac9x+\frac4{x-5}=1[/math]
[math]\frac{13x-45}{x(x-5)}=1[/math]
13x-45=x2-5x
x2-18x+45=0
x1=3<5 - корень, который приводит к нереальному решению, так как второму потребовалось бы на 5 дней меньше на работу.
x2=15
Ответ: 15
Постройте график функции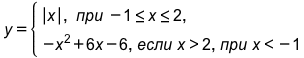 
и определите, при каких значениях а прямая y = a имеет с графиком ровно две общие точки.
Построим графики кусочно-заданной функции отдельно, а затем изобразим их на одной координатной плоскости.
y=|x| - два луча, выходящих из начала координат, являющихся биссектрисами прямых углов 1ой и 2ей четверти, но ограниченных условием -1≤x≤2
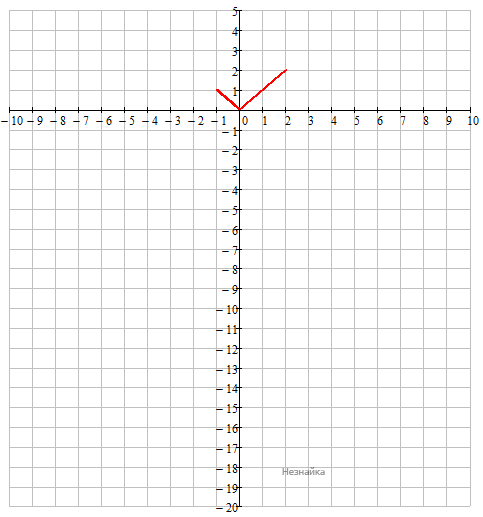
y=-x2+6x-6
y=-(x-3)2+3 - парабола, вершина (3;3), ветви вниз, без растяжений и сжатий. Строим для x>2 и x<-1.
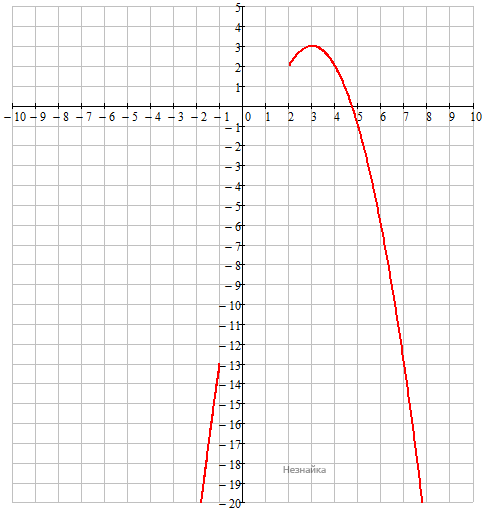
Совместим графики
Прямая y = a параллельна оси ОХ и имеет две общие точки с графиком в точке 0, при x<-13 и xє(1;3
Ответ: (-∞;-13),{0},(1;3)
Около окружности диаметром 15 описана равнобедренная трапеция с боковой стороной, равной 17. Найдите длину большего основания трапеции.
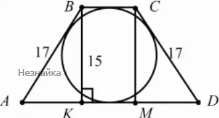
Так как около окружности описана равнобедренная трапеция, то высота трапеции равна диаметру. Проведем высоты BK и CM равные 15, причем BC=KM. По теореме Пифагора:
MD=√(CD2-CM2)=√(172-152)=8=AK
Так как в трапецию описана окружность, то
AD+BC=AB+CD
AK+KM+MD+BC=AB+CD
8+2BC+8=17+17
BC=9
AD=AK+KM+MD=8+9+8=25
Ответ: 25
Диагонали четырёхугольника АВСD взаимно перпендикулярны. Углы при вершинах В и С равны между собой. Докажите, что стороны АВ и СD параллельны.
Условие данной задачи составлено некорректно
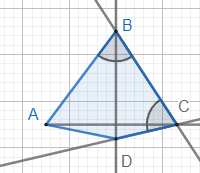
Здесь либо не хватает указания, что углы образованные диагоналями при вершинах В и С равны, либо чего то еще неведомого, но задуманного составителем заданий для ОГЭ. Так или иначе, надо решать это.
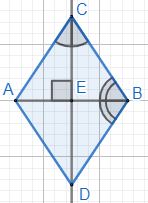
Прямоугольные треугольники ACE и BCE равны между собой по острому углу ∠ACE=∠BCE и общему катету CE. Тогда углы ∠CAE=∠CBE=∠DBE равны между собой.
Углы ∠CAE=∠DBE равны и являются накрест лежащими при прямых AC и BD и секущей AB, значит прямые AC и BD параллельны.
На продолжении стороны ВС треугольника АВС за точку В расположена точка Е так, что биссектрисы углов АЕС и АВС пересекаются в точке К, лежащей на стороне АС. Длина отрезка ВЕ = 1, длина отрезка ВС равна 2, градусная мера угла ЕКВ равна 30°. Найдите длину стороны АВ.
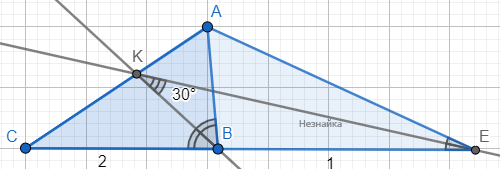Пусть ∠CBK=∠ABK=α, тогда ∠KBE=180º-α, ∠ABE=180º-2α. ∠BEK=180º-∠ЕКВ-∠KBE=180º-30º-(180º-α)=α-30º; ∠BEA=2∠BEK=2α-60º; ∠BAE=180º-∠ABE-∠BEA=180º-(180º-2α)-(2α-60º)=60º По свойству биссектрис BK и EK для треугольников ABC и AEC: [math]\frac{BC}{BA}=\frac{CK}{AK};\;\;\;\;\frac{EC}{EA}=\frac{CK}{AK}[/math] [math]EA=\frac{BA\cdot EC}{BC}=\frac32BA[/math] По теореме косинуса: BE2=BA2+EA2-2BA•EA•cos∠BAE 1=BA2+9/4•BA2-2•3/2•BA2•1/2 BA2=4/7 BA=2/√7 Ответ: 2/√7| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||