Вариант 7

Математика Профильный уровень

Часть 1

Ответом на задания 1—12 должно быть целое число или десятичная дробь.

По тарифному плану «Бессонный» интернет-провайдер каждый вечер снимает со счёта абонента 26 рублей. Если на счету осталось меньше 26 рублей, то на следующее утро интернет блокируется до пополнения счёта. Сегодня утром у Алексея на счету 800 рублей. Сколько дней (включая сегодняшний) он сможет пользоваться интернетом, не пополняя счёт?

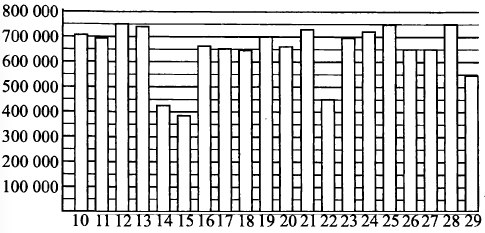
На диаграмме показано количество посетителей сайта новостей во все дни с 10 по 29 ноября 2012 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за день. Определите по диаграмме, сколько дней количество посетителей сайта новостей было наибольшим за указанный период.

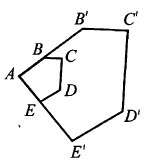
Периметры подобных многоугольников ABCDE и AB’C’D’E' относятся как 4 : 7. Площадь большего многоугольника равна 98. Найдите площадь меньшего многоугольника.

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка. Результат округлите до сотых.

Найдите корень уравнения [math]6^{x+3}=\frac1{216}[/math]

В треугольнике ABC угол C равен 90º, [math]\sin A=\frac{5\sqrt{34}}{34}[/math]. Найдите tg B.

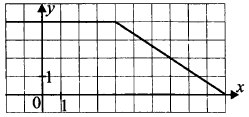
На рисунке изображён график функции у = f(x) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите F(10) — F(2).

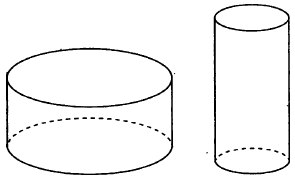
Дано два цилиндра. Объём первого цилиндра равен 72. У второго цилиндра высота в два раза больше, а радиус основания в три раза меньше, чем у первого. Найдите объём второго цилиндра.

Найдите значение выражения [math]y=11^{1,26}\times121^{0,37}[/math]

Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону U = U_o sin(ω t + φ), где t — время в секундах, амплитуда U_o = 10 В, частота ω = 150°/с, фаза φ = 30°. Датчик настроен так, что если напряжение в нём не ниже чем 5 В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?

Один токарь может выполнить заказ за 12 часов, второй — за 15 часов, а третий — за 20 часов. За сколько часов три токаря выполнят заказ, работая совместно?

Найдите точку максимума функции [math]y(x)=-x\sqrt x+6x[/math]

Часть 2.

При выполнении заданий 13—19 требуется записать полное решение и ответ.

а) Решите уравнение [math]\frac1{ctg^2x}-\frac1{sin\left(\frac\pi2-x\right)}=1[/math]

б) Найдите все корни этого уравнения, принадлежащие промежутку [math]\left[3\mathrm\pi;\frac{9\mathrm\pi}2\right][/math]

Показать ответ

Решение:

Данное уравнение приведем к виду: [math]\frac1{ctg^2x}-\frac1{\cos x}=1[/math]. Уравнение определено при условии [math]\sin x\neq0[/math] и [math]\cos x\neq0[/math]. Преобразуем уравнение: [math]tg^2x-\frac1{\cos^2x}=1[/math] => [math]\frac1{\cos^2x}-1-\frac1{\cos x}=1[/math]. Пусть [math]\frac1{\cos x}=t[/math], тогда получаем квадратное уравнение [math]t^2-t-2=0[/math] с корнями [math]t_1=-1;\;t_2=2[/math]. Имеем два уравнения [math]\frac1{\cos x}=-1;\;\frac1{\cos x}=2[/math] или [math]\cos x=-1;\;\cos x=\frac12.[/math] Решения первого уравнения не удовлетворяют условию [math]\sin x\neq0[/math]. Второе уравнение имеет решения: [math]x=\pm\frac{\mathrm\pi}3+2\mathrm{πn},\mathrm n\in\mathbb{Z}[/math]

б) Найдем корни в промежутке [math]\left[3\mathrm\pi;\frac{9\mathrm\pi}2\right][/math].

[math]\begin{array}{l}n=2,\;x=-\frac{\mathrm\pi}3+4\mathrm\pi=\frac{11\mathrm\pi}3\\\mathrm n=2,\;\mathrm x=\frac{\mathrm\pi}3+4\mathrm\pi=\frac{13\mathrm\pi}3\end{array}[/math]

Примечание: отбор корней можно произвести с помощью единичной окружности.

Ответ: а) [math]\pm\frac{\mathrm\pi}3+2\mathrm{πn},\;\mathrm n\in\mathbb{Z};[/math]

б) [math]\frac{11\mathrm\pi}3,\;\frac{13\mathrm\pi}3[/math]

Высота усеченного конуса равна [math]\frac{\sqrt3}2[/math]. Прямоугольный треугольник АВС с катетом ВС, равным 3, и углом А, равным 60°, расположен так, что вершина А лежит на окружности нижнего основания, а вершины В и С — на окружности верхнего основания. Найдите угол между плоскостью АВС и плоскостью основания усечённого конуса.

Показать ответ

Решение:

Не нарушая общности, можем считать, что [math]\angle С=90^\circ[/math]. Найдем катет [math]AC[/math] прямоугольного треугольника [math]ABC[/math]: [math]\frac{BC}{AC}=tgA;\;AC=\frac{BC}{tgA}=\frac3{\sqrt3}=\sqrt3[/math]

Угол между плоскостью ABC и плоскостью основания усеченного конуса равен углу [math]CAC_1[/math], где [math]C_1C[/math] - перпендикуляр к плоскости основания конуса (см. рисунок).

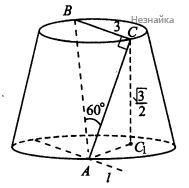
Действительно, плоскость [math]ABC[/math] пересекает плоскость верхнего основания конуса по прямой [math]BC[/math], а нижнего основания конуса по прямой [math]l[/math], значит [math]l\parallel BC[/math]. Так как [math]AC\perp BC[/math], то [math]AC\perp l[/math]. [math]AС_1[/math] - проекция [math]AC[/math] на плоскость нижнего основания конуса, следовательно, [math]AC_1\perp l[/math] по теореме о трех перпендикулярах. [math]\angle CAC_1[/math] найдем из прямоугольного треугольника [math]ACC_1[/math]. [math]\sin\angle CAC_1=\frac{CC_1}{AC}=\frac12[/math], [math]\angle CAC_1=30^\circ[/math].

Ответ: [math]30^\circ[/math]

Решите систему неравенств [math]\left\{\begin{array}{l}\vert\log_3(9-x^2)-5\vert\;+\;\log_3(9-x^2)\geq6x^2-x^4\\\log_{3-x}(\log_4\frac{x+5}{x+2})\geq0\end{array}\right.[/math]

Показать ответ

Решение:

Найдем решения первого неравенства системы.

Из условия [math]9-x^2>0[/math] получаем, что неравенство определено для [math]-3<x<3[/math]. При таких значениях справедливо неравенство: [math]\log_3(9-x^2)\leq\log_39=2[/math]

Значит, [math]\log_3(9-x^2)-5<0[/math] при [math]x\in(-3;3)[/math], и первое неравенство системы приводится к виду [math]5-\log_3(9-x^2)+\log_3(9-x^2)\geq6x^2-x^4[/math] или [math]x^4-6x^2+5\geq0.[/math]

Пусть [math]x^2=t[/math], тогда получаем квадратное неравенство [math]t^2-6t+5\geq0[/math], которое имеет решения [math]t\leq1;\;t\geq5[/math]. Далее из простейших неравенств [math]x^2\leq1;\;x^2\geq5[/math] находим значения [math]x\in(-\infty;-\sqrt5\rbrack\cup\lbrack-1;1\rbrack\cup\lbrack\sqrt5;+\infty)[/math]. Учитывая ограничение [math]-3<x<3[/math] получаем решения первого неравенства системы: [math]x\in(-3;-\sqrt5\rbrack\cup\lbrack-1;1\rbrack\cup\lbrack\sqrt5;3)[/math]

Найдем область определения второго неравенства системы.

[math]\left\{\begin{array}{l}\begin{array}{c}3-x>0\\3-x\neq1\\\frac{x+5}{x+2}>0\end{array}\\\log_4\frac{x+5}{x+2}>0\end{array}\right.\left\{\begin{array}{l}\begin{array}{c}x\neq2,\;x<3\end{array}\\\frac{x+5}{x+2}>1\end{array}\right.[/math] [math]x\in(-2;2)\cup(2;3)[/math]

Используя рационализацию второго неравенства на его области определения, получаем:

[math]\log_{3-x}(\log_4\frac{x+5}{x+2})\geq0[/math]

[math](3-x-1)(\log_4\frac{x+5}{x+2})-1)\geq0;[/math]

[math](2-x)(4-1)(\frac{x+5}{x+2}-4)\geq0;[/math]

[math]\frac{(x-2)(x+1)}{(x+2)}\geq0[/math]

Для решения последнего неравенства применим метод интервалов. Учитывая ОДЗ получим [math]x\in(-2;-1\rbrack\cup(2;3).[/math]

Найдем общую часть полученных решений неравенств системы: [math]\left\{-1\right\}\cup\lbrack\sqrt5;3)[/math]

Ответ: [math]\left\{-1\right\}\cup\lbrack\sqrt5;3)[/math]

Равнобедренный треугольник АВС вписан в окружность радиуса R, [math]\angle ABC=\alpha[/math]. Параллельно основанию АС проведена средняя линия, продолженная до пересечения с окружностью в точках P и K.

а) Докажите, что высота ВН треугольника АВС [math]BH=2R\cos^2\frac\alpha2[/math]

б) Найдите отношение площади треугольника АВС к площади треугольника КВР, если [math]\angle ABC=120^\circ[/math].

Показать ответ

Решение:

а) В [math]\bigtriangleup ABC[/math] по теореме синусов

[math]\frac{AC}{\sin\angle ABC}=2R,\;\frac{AC}{\sin\alpha}=2R,\;AC=2AH,\;2AH=2R\sin\alpha,\;AH=R\sin\alpha[/math] (см. рисунок)

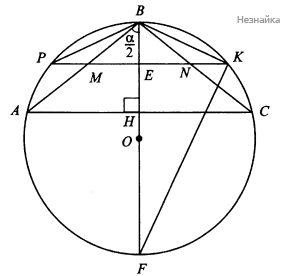
В [math]\bigtriangleup ABH:\;tg\angle ABH=\frac{AH}{BH},\;AH=BH\times tg\angle ABH=BH\times tg\;\frac\alpha2.[/math]

Имеем [math]R\sin\alpha=BHtg\frac\alpha2.[/math]

[math]BH=\frac{2R\sin{\displaystyle\frac\alpha2}\cos{\displaystyle\frac\alpha2}\cos{\displaystyle\frac\alpha2}}{\sin{\displaystyle\frac a2}}=2R\cos^2\frac\alpha2[/math], что и требовалось доказать

б) [math]S_{ABC}=\frac12\times AC\times BH=\frac12\times2R\sin\alpha\times2R\cos^2\frac\alpha2=2R^2\cos^2\frac\alpha2\sin\alpha.[/math]

[math]S_{KBP}=\frac12PK\times BE.[/math] По условию [math]MN[/math] - средняя линия [math]\bigtriangleup ABC[/math]? значит [math]BE=\frac12BH=R\cos^2\frac\alpha2.[/math] Из прямоугольного треугольника [math]BKF[/math] по свойству высоты, проведенной из вершины прямого угла

[math]KE^2=BE\times FE=R\cos^2\frac\alpha2(2R-R\cos^2\frac\alpha2)=[/math]

[math]=R^2\cos^2(1+1-\cos^2\frac\alpha2)=R^2\cos^2\frac\alpha2(1+\sin^2\frac\alpha2).[/math]

[math]PK=2KE=2R\cos\frac\alpha2\sqrt{1+\sin^2\frac\alpha2}[/math]

[math]S_{KPB}=\frac12\times2R\cos\frac\alpha2\sqrt{1+\sin^2\frac\alpha2}\times R\cos^2\frac\alpha2=R^2\cos^3\frac\alpha2\sqrt{1+\sin^2\frac\alpha2}.[/math]

[math]\frac{S_{ABC}}{S_{KBP}}=\frac{2R^2\cos^2{\displaystyle\frac\alpha2}\sin\alpha}{R^2\cos^3{\displaystyle\frac\alpha2}\sqrt{1+\sin^2{\displaystyle\frac\alpha2}}}=\frac{2\sin\alpha}{\cos{\displaystyle\frac\alpha2}\sqrt{1+\sin^2{\displaystyle\frac\alpha2}}}=\frac{4\sin{\displaystyle\frac\alpha2}}{\sqrt{1+\sin^2{\displaystyle\frac\alpha2}}}.[/math]

По условию [math]\alpha=120^\circ,[/math]

Ответ: [math]\frac{4\sqrt{21}}7[/math]

Прибыль «Незнайки» к концу года составила 9 408 000 рублей. Совет акционеров постановил распределить эту прибыль следующим образом: А рублей направить в фонд развития предприятия, 30% от А использовать для выплаты дивидендов акционерам, а 10% от А использовать на выплаты премий сотрудникам. Кроме того, было решено дополнительно выпустить акции для продажи на бирже ценных бумаг на сумму, равную половине суммы выплаченных дивидендов, в количестве 150 обыкновенных и 100 привилегированных (в 1,5 раза более дорогих) акций. Определите стоимость одной привилегированной акции.

Показать ответ

Решение:

Пусть [math]x[/math] рублей часть прибыли, направленная в фонд развития предприятия, тогда [math]\frac{30}{100}x[/math] рублей было направлено на выплату дивидендов, [math]\frac{10}{100}x[/math] рублей - на выплату премий сотрудникам. Зная, что прибыль составила [math]9408000[/math] рублей, составим решим уравнение.

[math]x+\frac3{10}x+\frac1{10}x=9408000[/math]

[math]x=6720000[/math]

В фонд развития предприятия было направлено 6720000 рублей, на дивиденды - 2016000 рублей. 672000 - на премии сотрудникам.

Обозначим стоимость обыкновенных акций через t, тогда [math]\begin{array}{l}150t+100\times1,5t=0,5\times2016000\\t=3360\end{array}[/math]

3360 рублей стоит обыкновенная акция.

[math]3360\times1,5=5040[/math] стоит привилегированная акция

Ответ: 5040.

Найдите все значения а, для каждого из которых уравнение [math]x^6+(3a-3\vert x\vert-a^2)^3+x^2=3\vert x\vert-3a+a^2[/math] имеет четыре различных решения.

Показать ответ

Решение:

Приведем данное уравнение к виду:

Пусть [math]\left|x\right|=t[/math], тогда получим квадратное уравнение [math]t^2-3t+3a-a^2=0,[/math] имеющее корни [math]t=a,\;t=3-a[/math]. Отсюда получаем [math]\left|x\right|=a,\;\left|x\right|=3-a[/math]. Построим графики функций [math]a(x)=\left|x\right|[/math] и [math]a(x)=3-\left|x\right|[/math] (см. рисунок). Первый график имеет "вершину" (0;0), а второй - (0;3). Решая систему [math]\left\{\begin{array}{l}a=\left|x\right|\\a=3-\left|x\right|\end{array}\right.[/math] найдем координаты двух общих точек: (-1,5;1,5) и (1,5; 1,5).

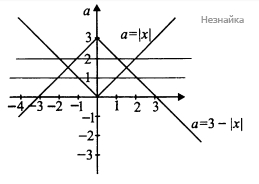
Рассмотрим семейство горизонтальных прямых.

При [math]a\in(0;1,5)\cup(1,5;3)[/math] эти прямые пересекают построенный график ровно в 4 точках. Значит, данное уравнение имеет ровно 4 различных решения при [math]a\in(0;1,5)\cup(1,5;3)[/math]

Ответ: [math](0;1,5)\cup(1,5;3)[/math]

Бесконечную последовательность b₁, b₂, b₃, ... назовём особенной, если все её члены — натуральные числа, причём для всех n b_n > b₁ + b₂ + ... +b _n—1

а) Может ли арифметическая прогрессия быть особенной последовательностью?

б) Может ли сумма цифр каждого члена особенной последовательности быть меньше 5?

в) Может ли для всех n выполняться неравенство [math]\frac{b_1+b_2+_\cdots+b_n}n\leq2015[/math]

Показать ответ

Решение:

а) Нет, не может. Предположим противное. Тогда найдется особенная последовательность [math]\left\{b_n\right\}[/math], для которой [math]b_n=b_{n-1}+d[/math] для некоторого натурального [math]d[/math], то есть [math]b_n-b_{n-1}>b_1+...+b_{n-2}>(n-2)b_1[/math], так как любой [math]b_j>b_{j-1}>...>b_1[/math] при [math]j\neq1.[/math]

Таким образом [math]d\geq(n-2)b_1,\;n\leq\frac d{b_1}+2[/math], что неверно в силу того, что [math]n[/math] - любое натуральное число, а [math]d[/math] и [math]b_1[/math] фиксированы.

б) Да, может. Приведем привер. Пусть [math]b_n=10^n[/math]. Сумма цифр любого [math]b_n[/math] равна 1, а [math]b_1+b_2+...+b_{n-1}=10+100+...+10^{n-1}=\frac{10^n-10}9<10^n[/math]

Предположим, что такая особенная последовательность существует, тогда, по условию задачи, имеем [math]b_2>b_1,[/math][math]b_3>b_1+b_2>2b_1,[/math][math]b_n>(n-1)b_1.[/math]

Значит, должно выполняться неравенство: [math]\frac{b_n}n(1+\frac{(n-1)n}2)<2015[/math], [math]\frac1n+\frac{n-1}2<\frac{2015}{b_1}[/math], которое неверно, поскольку [math]b_1[/math] фиксировано, а [math]n[/math] - произвольное натуральное число. Получили противоречие. Следовательно, такой последовательности не существует.

Ответ: а) нет; б) да; в) нет.

0 из 0

№	Ваш ответ	Ответ и решение	Первичный балл
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения.