Вариант 6
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Флакон герметика для автомобиля стоит 180 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 15%?
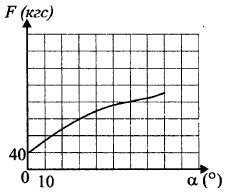
В аэропорту чемоданы пассажиров поднимают в зал багажа по транспортёрной ленте. При проектировании транспортёра необходимо учитывать допустимую силу натяжения ленты транспортёра. На рисунке изображена зависимость натяжения ленты от угла наклона транспортёра к горизонту при расчётной нагрузке. На оси абсцисс откладывается угол подъёма в градусах, на оси ординат — сила натяжения транспортёрной ленты (в килограммах силы). При каком угле наклона сила натяжения достигает 160 кгс? Ответ дайте в градусах.
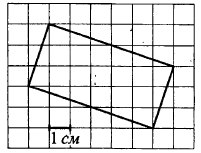
Найдите площадь прямоугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.
В люстре две одинаковые лампы. Вероятность перегорания каждой лампы в течение года равна 0,6. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит.
Найдите корень уравнения [math]\sqrt{\frac8{6x-96}}=\frac19[/math]
В треугольнике АВС угол С равен 90°, tg ВАС = [math]\frac{7\sqrt{15}}{15}[/math]. Найдите синус внешнего угла при вершине А.
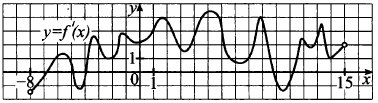
На рисунке изображён график у = f'(х) — производной функции f(х), определённой на интервале (—8; 15). Найдите количество точек минимума функции f(х), принадлежащих отрезку [1; 13].
Цилиндр описан около шара. Объём шара равен 18. Найдите объём цилиндра.
Найдите значение выражения: [math]y=\frac{49x^2-25}{7x+5}-7x[/math]
Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально, и на исследуемом интервале температура определяется по формуле T(t) = То + at + bt2, где t — время в минутах, То = 120 К, b = -1/4 K/мин2, а = 39,5 К/мин. Известно, что при температуре нагревателя свыше 1080 К прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.
Из пункта А в пункт В одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 60 км/ч, а вторую половину пути — со скоростью на 20 км/ч меньшей, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Найдите наибольшее значение функции [math]y=x\sqrt x-5x+5[/math] на отрезке [math]\left[1;25\right][/math].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math]\sin^2Зx-2\;\sin\;6x\;+\;3\cos^2\;Зx=0[/math].
б) Укажите все корни этого уравнения, принадлежащие промежутку [math]\left[-1;1\right][/math].
Решение:
[math]\sin^23x-4\sin3x\cos3x+3\cos^23x=0[/math]
а) Заметим, что при [math]\cos3x=0[/math] из основного тригонометрического тождества следует, что [math]\sin^23x=1[/math] и потому [math]\sin3x=\pm1[/math], а значит, уравнение превратится в неверное равенство. Разделим обе части на [math]\cos^23x[/math], получим [math]tg^2x-4tg3x+3=0[/math]. Сделаем замену [math]tg3x=t[/math], тогда [math]t^2-4t+3=0,\;t=1,t=3[/math]
[math]tg3x=1,\;x=\frac{\mathrm\pi}{12}+\frac{\mathrm{πk}}3,\;k\in\mathbb{Z}[/math]
[math]tg3x=3,\;x=\frac{arctg3}3+\frac{\mathrm{πn}}3,\;n\in\mathbb{Z}[/math]
б) [math]\begin{array}{l}k=0,\;x=\frac{\mathrm\pi}{12}\\k=-1,\;x=\frac{\mathrm\pi}{12}-\frac{\mathrm\pi}3=-\frac{\mathrm\pi}4\\n=0,\;x=\frac{arctg3}3\\n=1,\;x=\frac{arctg3}3-\frac{\mathrm\pi}3\end{array}[/math]
Ответ: а) [math]\frac{arctg3}3+\frac{\mathrm{πn}}3,\;n\in\mathbb{Z};[/math]
[math]\frac{\mathrm\pi}{12}+\frac{\mathrm{πk}}3,\;k\in\mathbb{Z};[/math]
б) [math]-\frac{\mathrm\pi}4,\;\frac{arctg3}3-\frac{\mathrm\pi}3,\;\frac{arctg3}3,\;\frac{\mathrm\pi}{12}[/math]
Высота усечённого конуса равна [math]\sqrt3[/math]. Прямоугольный треугольник АВС с углом А, равным 60°, и углом С, равным 90°, расположен так, что вершина А лежит на окружности нижнего основания, а вершины В и С — на окружности верхнего основания. Найдите АВ, если угол между плоскостью АВС и плоскостью основания усечённого конуса равен 60°.
Решение:
Угол между плоскостью [math]ABC[/math] и плоскостью основания усеченного конуса равен углу [math]CAC_1[/math], где [math]CC_1[/math] - перпендикуляр к плоскости основания конуса (см. рисунок)
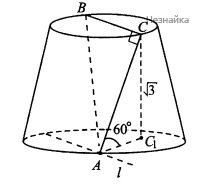
Действительно, плоскость [math]ABC[/math] пересекает плоскость верхнего основания конуса по прямой [math]BC[/math], а нижнего основания конуса по прямой [math]l[/math], значит [math]l\parallel BC[/math]. Так как [math]AC\perp BC[/math], то [math]AC\perp l[/math]. [math]AC_1[/math] - проекция [math]AC[/math] на плоскость нижнего основания конуса, следовательно, [math]AC_1\perp l[/math] по теореме о трех перпендикулярах. В прямоугольном треугольнике [math]ACC_1[/math] [math]\frac{CC_1}{AC}=\sin\angle CAC_1[/math], откуда [math]AC=\frac{CC_1}{\sin\angle CAC_1}=\frac{\sqrt3}{\sin60^\circ}=2[/math]
В прямоугольном треугольнике [math]ABC[/math] катет [math]AC[/math] лежит напротив угла в [math]30^\circ[/math], следовательно гипотенуза [math]AB=2AC=4[/math]
Ответ: [math]AB=4[/math]
Решите систему неравенств
[math]\left\{\begin{array}{l}\frac3{x-1}+\frac1{x+2}\leqslant\frac1{x-1}+\frac3{x+2},\\2\log_x3-3\log_3x\geqslant1.\end{array}\right.[/math]
Решение:
[math]\begin{array}{l}\frac3{x-1}+\frac1{x+2}\leq\frac1{x-1}+\frac3{x+2};\\\frac{3(x+2)+x-1}{(x-1)(x+2)}\leq\frac{x+2+3(x-1)}{(x-1)(x+2)};\\\frac6{(x-1)(x+2)}\leq0\\x\in(-2;1)\end{array}[/math]
Решим второе неравенство системы.
ОДЗ: [math]\left\{\begin{array}{l}x>0\\x\neq1\end{array}\right.[/math]
Пусть [math]\log_3x=t[/math], тогда [math]\frac2t-3t\geq1[/math]; [math]\frac{-3t^2-t+2}t\geq0[/math]
решив уравнение [math]3t^2+t-2=0[/math], получим [math]t_1=-1;\;t_2=\frac23[/math], тогда рассматриваемое неравенство примет вид [math]\frac{3(t-{\displaystyle\frac23})(t+1)}t\leq0[/math]. [math]t\in(-\infty;\;-1\rbrack\;\cup(0;\;\frac23\rbrack[/math]. Из условия [math]\log_3x\leq-1[/math] получим [math]x\leq\frac13[/math] и из условия [math]0\leq\log_3x\leq\frac23[/math] получим [math]x\in(1;\sqrt[3]9\rbrack[/math]. Учитывая ОДЗ, получим [math]x\in(0;\frac13\rbrack\cup(1;\sqrt[3]9\rbrack[/math]
Определим пересечение полученных решений первого и второго неравенства системы: [math]x\in(0;\frac13\rbrack[/math]
Ответ: (0; 1/3]
Две окружности с центрами О и О1 радиусы которых 2 и 6, касаются внешним образом, АС — их общая внешняя касательная.
а) Докажите, что угол СО1О равен 60°, где О1С — радиус, проведённый в точку касания.
б) Найдите периметр фигуры, образованной внешними касательными и внешними дугами окружностей.
Решение:
а) Заметим, что [math]OA\perp AC[/math] и [math]O_1C\perp AC[/math] по свойству радиусов, проведеных в точку касания (см. рисунок). Опустим [math]OK\perp O_1C[/math], тогда [math]OACK[/math] - прямоугольник, [math]CK=OA=2,[/math][math]O_1K=O_1C-CK=6-2=4.[/math] Обозначим буквой [math]M[/math] точку касания окружностей, тогда [math]OM=2,\;O_1M=6,\;OO_1=8.\;[/math] В прямоугольном треугольнике [math]O_1OK[/math] выполняется соотношение [math]\frac{O_1K}{OO_1}=\frac12[/math], следовательно, [math]\angle O_1OK=30^\circ.[/math] Тогда [math]\angle OO_1K=90^\circ-\angle O_1OK=60^\circ,[/math][math]\angle CO_1O=60^\circ,[/math] что и требовалось доказать.
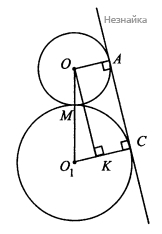
б) [math]\angle O_1OA=180^\circ-60^0=120^\circ.[/math] Градусная мера внешней дуги внешней окружности равна[math]360^\circ-120^\circ-120^\circ=120^\circ[/math]. Градусная мера внешней дуги большей окружности равна [math]360^\circ-60^\circ-60^\circ=240^\circ[/math]. Значит, длина внешней внешней дуги меньшей окружности равна [math]\begin{array}{l}2\mathrm\pi\times2\times\frac{120^\circ}{360^\circ}=\frac{4\mathrm\pi}3\\\end{array}[/math]. Длина внешней дуги большей окружности равна [math]\begin{array}{l}2\mathrm\pi\times6\times\frac{240^\circ}{360^\circ}=8\mathrm\pi\\\end{array}[/math]. Из треугольника [math]\begin{array}{l}{\mathrm O}_1\mathrm{OK}\\\end{array}[/math] по теореме Пифагора [math]\begin{array}{l}\mathrm{OK}=\sqrt{{\mathrm{OO}}_1^2-{\mathrm O}_1\mathrm K^2}=\sqrt{48}=4\sqrt3\\\end{array}[/math]. [math]\begin{array}{l}\mathrm{AC}={\mathrm A}_1{\mathrm C}_1=4\sqrt3\\\end{array}[/math]
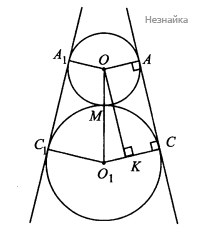
Искомый периметр равен: [math]\begin{array}{l}\frac{4\mathrm\pi}3+4\sqrt3+8\mathrm\pi+4\sqrt3=8\sqrt3+\frac{28\mathrm\pi}3\\\end{array}[/math]
Ответ: [math]\frac{28\mathrm\pi}3+8\sqrt3[/math]
Холдинг «Вертолёты России» планирует выпустить в первом квартале 20% годового плана, во втором — увеличить производство в 1,5 раза, в четвёртом выпустить 102 вертолёта. В третьем квартале, во время отпусков, как показывает статистика, выпускается половина от среднего арифметического количества выпускаемых вертолётов во втором и четвёртом кварталах. Какое количество вертолётов планируется выпустить холдингом в третьем квартале?
Решение:
Пусть [math]x[/math] вертолетов планируется выпустить за год. Тогда в первом квартале выпустят [math]0,2x[/math] вертолетов, во втором квартале [math]0,3x[/math], в третьем [math]\frac12\times\frac{0,3x+102}2[/math]. Составим и решим уравнение:
[math]\begin{array}{l}0,2x+0,3x+\frac{0,3x+102}4+102=x\\x=300\end{array}[/math]
[math]\frac{0,3\times300+102}4=48[/math] вертолетов планируется выпустить в третьем квартале.
Ответ: [math]48[/math]
Найдите все значения параметра а, при которых уравнение [math]\log_\frac1a(\sqrt{x^2+ax+10}+1)\lg\left(x^2+ax+11\right)+2log_a2=0[/math] имеет нечетное количество решений.
Решение:
ОДЗ: [math]\left\{\begin{array}{l}\;\;\;\;\;\;\;\;\;a>0,\\\begin{array}{c}a\neq1,\\x^2+ax+10\geq0\\x^2+ax+11>0\end{array}\end{array}\right.[/math][math]\left\{\begin{array}{l}\;\;\;\;\;\;\;\;\;a>0,\\\begin{array}{c}a\neq1,\\x^2+ax+10\geq0\end{array}\end{array}\right.[/math]
Обозначим [math]x+\frac\alpha2=t.[/math]
Уравнение примет вид
[math]log_\frac1a(\sqrt{t^2+10-\frac{a^2}4}+1)lg(t^2+11-\frac{a^2}4)+2\log_a2=0.[/math]
Функция [math]f(t)=log_\frac1a(\sqrt{t^2+10-\frac{a^2}4}+1)lg(t^2+11-\frac{a^2}4)+2\log_a2[/math] - четная
Исходное уравнение имеет ровно одно решение при [math]t=0[/math], в противном случае будет четное число решений,что противоречит условию задачи.
Имеем [math]f(0)=0.[/math]
[math]\log_\frac1a(\sqrt{10-\frac{a^2}4}+1)lg(11-\frac{a^2}4)+2\log_a2=0. (1)[/math]
Пусть [math]\sqrt{10-\frac{a^2}2}=b,\;b\geq0.[/math] Тогда уравнение (1) принимает вид: [math]\begin{array}{l}-\log_a(b+1)lg(b^2+1)+\log_a4=0,\\\log_2(b+1)\times log_2(b^2+1)=\log_24\times\log_210.\;(2)\end{array}[/math]
Если [math]b=0[/math], то получаем противоречие, поэтому [math]b>0,\;b+1>1[/math] и [math]b^2+1>1[/math]. Отсюда следует, что функции [math]g(b)=\log_2(b+1)[/math] и [math]f(b)=\log_2(b^2+1)[/math] являются возрастающими положительными функциями. Их произведение является тоже возрастающей функцией.
Если [math]b+1=4[/math] и [math]b^2+1=10[/math], то [math]b=3[/math] удовлетворяет (2).
Других решений уравнение (2) не имеет, так как права часть уравнения (2) является константой.
Ответ: [math]a=2[/math]
На доске написано более 40, но менее 48 целых чисел. Среднее арифметическое этих чисел равно -3, среднее арифметическое всех положительных из них равно 4, а среднее арифметическое всех отрицательных из них равно -8.
а) Сколько чисел написано на доске?
б) Каких чисел написано больше: положительных или отрицательных?
в) Какое наибольшее количество положительных чисел может быть среди них?
Пусть среди написанных чисел k положительных, l отрицательных и m нулей. Сумма набора чисел равна количеству чисел в этом наборе, умноженному на его среднее арифметическое, поэтому [math]4k-8l+0\times m=-3(k+l+m).[/math]
а) Заметим, что в левой части приведённого выше равенства каждое слагаемое делится на 4, поэтому
[math]k+l+m[/math] — количество целых чисел — делится на 4. По условию [math]40<k+l+m<48,[/math], поэтому [math]k+l+m=44[/math]. Таким образом, написано 44 числа.
б) Приведем равенство [math]4k-8l=-3(k+l+m)[/math] к виду [math]5l=7k+3m[/math]. Так как [math]m\geq0[/math], получаем, что [math]5l\geq7k[/math], откуда [math]l>k[/math]. Следовательно, отрицательных чисел больше, чем положительных.
в) Подставим [math]k+l+m=44[/math] в правую часть равенства [math]4k-8l=-3(k+l+m):\;4k-8l=-132,[/math] откуда [math]k=2l-33[/math]. Так как [math]k+l\leq44[/math], получаем: [math]3l-33\leq44;\;3l\leq77;\;l\leq25;\;k=2l-33\leq17[/math], то есть положительных чисел не более 17.
Приведём пример, когда положительных чисел ровно 17. Пусть на доске 17 раз написано число 4, 25 раз написано число -8 и 2 раза написан 0. Тогда [math]\frac{4\times17-8\times25}{44}=-3[/math], указанный набор удовлетворяет всем условиям задачи.
Ответ: а) 44; б) отрицательных; в) 17.
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||