Вариант 3
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Чтобы покрасить 8 метров забора, необходима одна 5-литровая банка краски. Сколько понадобится таких банок для покраски 34-метрового забора?
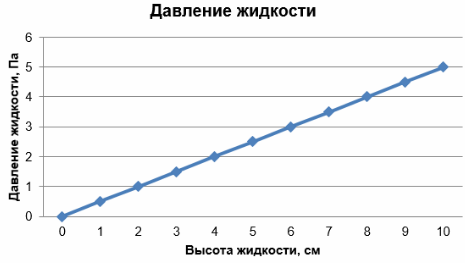
На рисунке точками показана зависимость давления от высоты столба жидкости. По горизонтали отмечается высота столба (в см), по вертикали – давление (в Па). На сколько давление (в Па) будет больше при высоте столба жидкости 9 см, чем при высоте 4 см?
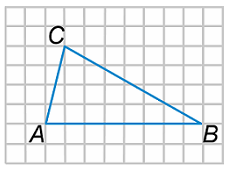
На клетчатой бумаге с размером клетки 1 см × 1 см изображён треугольник. Найдите длину медианы, проведенной из вершины C. Ответ дайте в см.
Для рассады имеются два сорта помидоров: красный «Аврора» — 48 семян, жёлтый «Ураган» — 32 семени. Найдите вероятность того, что случайно выбранный саженец даст плод жёлтого цвета, при условии, что все семена взойдут.
Решите уравнение [math]tg\frac{\pi x}6=\sqrt3[/math]. В ответе укажите наибольший отрицательный корень.
В равнобедренном треугольнике ABC с основанием AC = [math]6\sqrt3[/math] м проведена высота BH = 3 м. Найдите радиус окружности, описанной около данного треугольника (в м).
Тело движется прямолинейно по закону [math]x(t)=\frac43t^3-13t^2+56,25t-13[/math], где x (t) измеряется в метрах, а время t — в секундах. В какой момент времени (в с) скорость будет равна 14 м/с?
На поверхности шара с центром O взяты две точки F и L. Угол FOL равен 90°, FL = [math]6\sqrt2[/math] м. Найдите объем шара V (в м3), в ответе укажите [math]\frac V\pi[/math].
Вычислите [math]\frac{log_7216\cdot log_67}{log_2384-log_224}[/math]
Насос выбрасывает струю воды под напором. Необходимая мощность для выбрасывания этой струи вычисляется по формуле [math]P=\frac\pi8\cdot p\cdot d^2\cdot v^3[/math]. Найдите диаметр струи d (в м), если скорость струи воды v = 14 м/c, мощность насоса равна 1646,4 Вт, плотность воды p = 1000 кг/м3, [math]\pi[/math] принять равным 3.
В офисе имеются два принтера: лазерный и струйный. Скорость первого на 9 стр./мин больше второго. Найдите скорость лазерного принтера (в стр./ мин), если, работая одновременно, они напечатали 585 страниц за 15 мин.
Найдите точку максимума функции [math]f(x)=\frac53x^6+\frac25x^5-\frac{35}3x^3-\frac72x^2+105[/math], принадлежащую промежутку [math]\left[-1;1\right][/math].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
Дано уравнение [math]9^{\sin x\cdot tgx}\cdot27^{tgx}=\left(\frac13\right)^\frac1{\cos x}[/math].
А) Решите уравнение.
Б) Найдите его корни, принадлежащие отрезку [6π; 7,5π].
А) Преобразуем левую и правую части:
[math]3^\frac{2sin^2x}{cosx}\cdot3^\frac{3sinx}{cosx}=3^\frac{-1}{cosx}[/math]
[math]3^\frac{2sin^2x+3sinx+1}{cosx}=3^0[/math]
Основания равны, значит и показатели при этих основаниях тоже равны. Получим:
[math]2sin^2x+3sinx+1=0[/math]
Осуществим замену. Пусть t=sinx
[math]2t^2+3t+1=0[/math]
[math]t_1=-1[/math][math]t_2=-\frac12[/math]
Обратная замена:
[math]sinx=-1[/math]
[math]x=-\frac\pi2+2\pi n[/math]
[math]sinx=-\frac12[/math]
[math]x=(-1)^{k+1}\frac\pi6+\pi k[/math], [math]k\in Z[/math]
Б) Нанесем на числовую прямую наши корни:
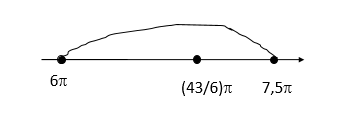
В отрезок вошел только один корень [math]\frac{43\pi}6[/math]
Ответ: А) [math]\left(-1\right)^{k+1}\cdot\frac\pi6+\pi k,\;k\in Z[/math]
Б) [math]\frac{43\pi}6[/math]
В правильной четырехугольной пирамиде PABCD сторона основания равна 20, а высота пирамиды равна 11,25. Через ребро АВ под углом β к плоскости АВС проведена плоскость α. Известно, что [math]tg\beta=\frac34[/math].
А) Докажите, что плоскость α делит ребро РС в отношении 1:4, считая от точки Р.
Б) Найдите площадь сечения пирамиды плоскостью α.
Решение:
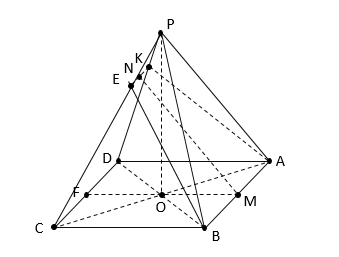
А) Плоскость [math]\alpha[/math] пересекает грань [math]CPD[/math] по прямой [math]EK\parallel AB[/math]. т.к. пирамида правильна, то [math]EB=KA[/math], т.е. сечение [math]AKEB[/math] – равнобедренная трапеция.
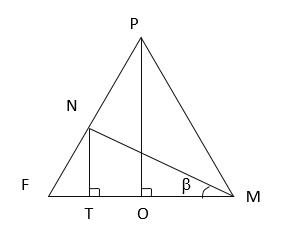
[math]\angle NMF[/math] – линейный угол двугранного угла [math]CABN[/math], т.к. [math]\alpha\cap(ABC)=AB[/math].
[math]FM\perp AB[/math], [math]M[/math] – середина [math]AB[/math]
[math]NM\perp AB[/math] (высота трапеции)
[math]O[/math] – середина [math]FM[/math],т.е [math]FO=OM=10[/math]
Из [math]\bigtriangleup FPO[/math] : [math]tg\angle F=\frac{PO}{OF}=\frac{45}{4\cdot10}=\frac98[/math]
Пусть [math]FT=x[/math], тогда [math]TM=20-x[/math]
Из [math]\bigtriangleup FNT[/math] : [math]NT=FT\;tg\angle F=\frac98x[/math]
Из [math]\bigtriangleup TNM[/math] : [math]NT=TM\;tg\beta=(20-x)\cdot\frac34[/math]
[math]\frac98x=(20-x)\cdot\frac34[/math]
[math]x=8[/math]
[math]FN=8[/math], [math]NT=9[/math]
[math]ER=NT=9[/math]
[math]\bigtriangleup COP\sim\bigtriangleup CER[/math], [math]\frac{CE}{CP}=\frac{ER}{PO}=\frac9{\frac{45}4}=\frac45[/math][math]\Rightarrow CE:EP=4:1[/math] или [math]EP:EC=1:4[/math]
Б) Из [math]\bigtriangleup NTM[/math]: [math]NT[/math]=9,[math]TM=12[/math], [math]NM^2=9^2+12^2=81+144=225[/math],[math]NM=15[/math]
[math]\bigtriangleup PEK\sim\bigtriangleup PCD[/math]
[math]\frac{PE}{PC}=\frac{EK}{CD}=\frac15\Rightarrow EK=\frac15CD=\frac15\cdot20=4[/math]
[math]S_{трап}=\frac{AB+EK}2\cdot NM=\frac{20+4}{20}\cdot15=12\ast15=180[/math]
Ответ: 180
Решите неравенство [math]\frac{\left(2^x-2\right)^3}{2^{x+2}-12}\geq\frac{8^x-4^{x+1}+2^{x+2}}{9-4^x}[/math].
Решение:
[math]\frac{2^{3x}-6\cdot2^{2x}+12\cdot2^x-2^3}{4(2^x-3)}\geq\frac{2^{3x}-4\cdot2^{2x}+2\cdot2^x}{(3-2^x)(3+2^x)}[/math]
[math]\frac{(2^x-2)^3(3+2^x)+4\cdot2^x(2^x-2)^2}{4(2^x-3)(2^x+3)}\geq0[/math]
[math]\frac{(2^x-2)^2((2^x-2)(3+2^x)+4\cdot2^x)}{4(2^x-3)(2^x+3)}\geq0[/math]
[math]\frac{(2^x-2)^2(2^x+5\cdot2^x-6)}{4(2^x-3)(2^x+3)}\geq0[/math]
[math]2^x=2[/math]
Нули числителя: x=1 – корень кратности 2
[math]2^{2x}+5\cdot2^x-6=0[/math]
[math]2^x=1[/math]
[math]x=0[/math]
[math]2^x=-6[/math]. Корней нет, так как -6<0
Нули знаменателя: [math]x=log_23[/math]
Решим на числовой прямой:
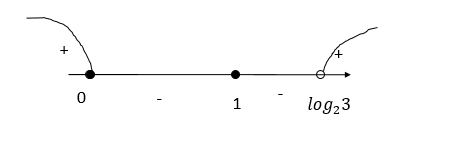
Ответ: (-∞; 0]⋃{1}⋃(log23; +∞)
Первая окружность, вписанная в равнобедренный треугольник АВС, касается основания АС в точке М. Вторая окружность касается основания АС и продолжений боковых сторон.
А) Докажите, что длина основания треугольника является средним геометрическим диаметров первой и второй окружностей.
Б) Найдите радиус второй окружности, если радиус первой равен 3, а ВМ=8.
Решение:
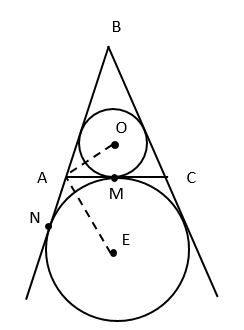
А) [math]AO[/math] – биссектриса [math]\angle BAM[/math] ( по свойству касательных , проведенных из одной точки)
[math]AE[/math] – биссектриса [math]\angle MAN[/math]
[math]\angle BAM+\angle MAN=180^\circ[/math], [math]2\angle OAM+2\angle MAE=180^\circ[/math]
[math]\angle OAM+\angle MAE=90^\circ[/math], т.е. [math]\bigtriangleup OAE[/math] – прямоугольный
[math]AM\perp OM[/math], т.к. [math]BM[/math] – высота,медиана равнобедренного треугольника [math]\bigtriangleup АВС[/math]
[math]М[/math] – середина [math]АС[/math]
Вторая окружность, также касается [math]АС[/math] в точке [math]М[/math]
[math]АМ[/math] – высота [math]\bigtriangleup АОЕ[/math], проведенная из прямого угла, значит [math]АМ=\sqrt{МО\cdot МЕ}[/math]
[math]АМ=\frac12АС[/math],[math]МО=\frac12d_1[/math], [math]МE=\frac12d_2[/math], тогда [math]\frac12АС=\sqrt{\frac12d_1\cdot\frac12d_1}=\frac12\sqrt{d_1\cdot d_2}[/math]
Б) Пусть [math]\angle ОАМ=\alpha[/math], тогда [math]\angle ВАМ=2\alpha[/math]
Пусть [math]МЕ=x[/math], [math]AM=y[/math]
Из [math]\bigtriangleup ABM[/math]: [math]tg2\alpha=\frac{BM}{AM}=\frac8y[/math]
Из [math]\bigtriangleup OAM[/math]:[math]tg\alpha=\frac{OM}{AM}=\frac3y[/math]
[math]tg2\alpha=\frac{2tg\alpha}{1-tg^2\alpha}[/math]
[math]\frac8y=\frac{2\cdot\frac3y}{1-\frac9{y^2}}[/math]
[math]\frac8y=\frac{6y}{y^2-9}[/math]
[math]8(y^2-9)=6y^2[/math]
[math]8y^2-6y^2=8\cdot9[/math]
[math]y=6[/math]
[math]AM=6[/math]
[math]AM=\sqrt{OM\cdot ME}[/math]
[math]6=\sqrt{3x}[/math]
[math]ME=x=12[/math]
Ответ:12
Из пункта А в пункт В со скоростью 80 км/ч выехал первый автомобиль, а через некоторое время с постоянной скоростью - второй. После остановки на 20 мин в пункте В второй автомобиль поехал с той же скоростью назад. Через 48 км он встретил первый автомобиль, шедший навстречу, и был на расстоянии 120 км от В в тот момент, когда в пункт В прибыл первый автомобиль. Найти расстояние от А до места первой встречи, если расстояние между пунктами А и В равно 480 км.
Решение: найдем время,потраченное вторым автомобилем до первой встречи из пункта В: [math]t=\frac{48}{80}[/math]=0.6
Вычислим скорость второго автомобиля: [math]v_2=\frac{120-48}{0.6}=120[/math]
Получим, что первый на весь путь АВ потратил [math]t_1=\frac{48}{80}=6[/math] , а второй -[math]t_2=\frac{48}{120}=4[/math]
Время, за которое проехал второй до места второй встречи с первым: [math]\frac{48}{120}=0,4[/math] часа [math]=24[/math] мин
Время, которое второй потратил до второй встречи равно 4 часа + 20 мин + 24 мин = 4 часа 44 мин, а первого- 6 часов – 0,6 = 5,4 часа = 5 часов 24 мин
Найдем время, на которое второй выехал позже: 5 часов 24 – 4 часа 44 мин=40 мин
Найдем время, которое потратил второй до места первой встречи: [math]\frac{3200}{\frac{60}{120-80}}=\frac86[/math] (час)
В итоге получим расстояние от А до места первой встречи [math]\frac{120\cdot8}6=160[/math]км
Ответ:160 км
Для каждого значения параметра а найдите точку максимума функции f(x) = x3(3x - 8a) + 6(a2 - 1)x2.
Решение: преобразуем функцию
[math]f(x)=x^2(3x^2-8ax+6(a^2-1))[/math] ветви вверх
Возьмем производную:
[math]f'(x)=12x^3-24ax^2+12(a^2-1)x[/math]
[math]f'(x)=0[/math]
x=0
[math]x^2-2ax+(a^2-1)=0[/math]
[math]D=a^2-(a^2-1)=1[/math][math]x_1=a+1[/math],[math]x_2=a-1[/math]
1 сл: 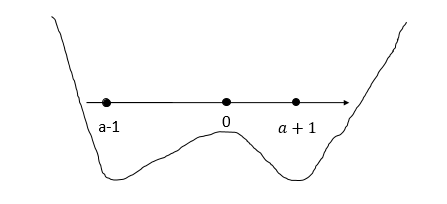
a-1 0.т.е. при [math]-1<a<1[/math] x=0-экстремум
2 сл: 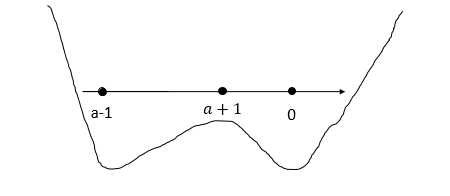
a-1<0 и a+1<0.т.е. при а < -1 xmax = a+1
3 сл: 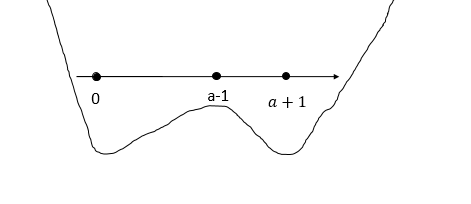
a-1>0 и a+1>0.т.е при [math]a>1[/math] xmax = a-1
4 сл: [math]a=\pm1[/math]. тогда имеем корень х=0- корень кратности 2, корень х=2 или х=-2. Значит, имеем функцию, не имеющую максимум функции
Ответ: при а < -1 xmax = a+1, при [math]a>1[/math] xmax = a-1, при [math]-1<a<1[/math] xmax = 0.
Дан клетчатый квадрат размером 6х6.

А) Можно ли этот квадрат разрезать на десять попарно различных клетчатых многоугольников?
Б) Можно ли этот квадрат разрезать на одиннадцать попарно различных клетчатых многоугольников?
B) На какое наибольшее число попарно различных клетчатых прямоугольников можно разрезать этот квадрат?
Решение:
А) Чтобы понять, сколько фигурок можно поместить в этот квадрат и как их разместить, необходимо применить два способа: посчитать математически, подобрать слагаемые с учетом того, чтобы одно и то же слагаемое не повторилось больше, чем возможно собрать из этого количества квадратиков вариантов; рассмотреть все возможные варианты фигурок з предложенного количества квадратиков. Таким образом, мы получим, что 36= 6*1+5*1+4*4+3*2+2*1+1*1
Возможные варианты:

Получим следующее решение:

Б) Аналогично решим задачу, по условию которой требуется одиннадцать различных многоугольников. Однако, данная задача не имеет решения
В) Найдем максимально возможное количество прямоугольников и получим следующее выражение: 36=1+2+3+4*2+5+6*2

Ответ:А) да; Б) нет; В) 8
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||