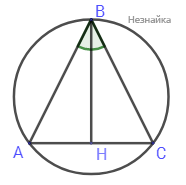
В прямоугольном треугольнике AHB: AH=AC/2=6√3/2=3√3

[math]tg\angle ABH=\frac{AH}{BH}=\frac{3\sqrt3}3=\sqrt3\Rightarrow\angle ABH=60^\circ[/math]

Высота в равнобедренном треугольнике является биссектрисой, поэтому

[math]\angle ABC=2\cdot\angle ABH=2\cdot60^\circ=120^\circ[/math]

Найдем радиус описанной окружности по теореме синусов:

[math]R=\frac{AC\sqrt3}{2\cdot sin120^\circ}=\frac{6\sqrt3}{2\cdot\frac{\sqrt3}2}=6[/math]