Вариант 18
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Система навигации самолёта информирует пассажира о том, что полёт проходит на высоте 35 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30,5 см.
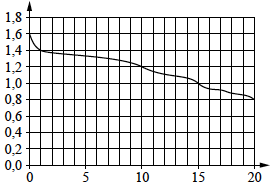
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, за сколько часов напряжение упадёт с 1,4 вольта до 1 вольта.
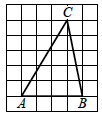
На клетчатой бумаге с размером клетки 1х1 изображён треугольник ABC . Найдите длину его высоты, опущенной на сторону AB .
Вероятность того, что новый сканер прослужит больше года, равна 0,94. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Найдите корень уравнения log8 (5x + 47) = 3.
Стороны параллелограмма равны 9 и 15. Высота, опущенная на меньшую из этих сторон, равна 10. Найдите высоту, опущенную на бо́льшую сторону параллелограмма.
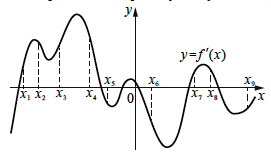
На рисунке изображён график y = f '(x) — производной функции f (x) . На оси абсцисс отмечено девять точек: x1 , x2 , x3 , x4 , x5 , x6 , x7 , x8 , x9 . Сколько из этих точек принадлежит промежуткам убывания функции f (x) ?
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.
Найдите значение выражения [math]\frac{\left(5^{\displaystyle\frac35}\cdot7^{\displaystyle\frac23}\right)^{15}}{35^9}[/math].
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением a = 4500 км/ч2. Скорость v (в км/ч) вычисляется по формуле [math]\nu=\sqrt{2la}[/math], где l — пройденный автомобилем путь (в км). Найдите, сколько километров проедет автомобиль к моменту, когда он разгонится до скорости 90 км/ч.
Первая труба наполняет резервуар на 48 минут дольше, чем вторая. Обе трубы, работая одновременно, наполняют этот же резервуар за 45 минут. За сколько минут наполняет этот резервуар одна вторая труба?
Найдите точку минимума функции y = (1 - 2x) cos x + 2sin x + 7 ,
принадлежащую промежутку [math]\left(0;\;\frac{\mathrm\pi}2\right)[/math].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math](\sqrt{x^2+2x-7}-1)\log_3(9+2x-x^2)=0[/math]
б) Найдите все корни этого уравнения, принадлежащие промежутку [math]\left[\log_35;2^\sqrt2\right][/math].
Решение:
а) Данное уравнение определено при условиях [math]\left\{\begin{array}{l}x^2+2x-7\geq0\\9+2x-x^2>0\end{array}\right.[/math] и расщепляется на 2 уравнения [math]\sqrt{x^2+2x-7}-1=0[/math] и [math]\log_3(9+2x-x^2)=0[/math]. Первое уравнение после возведения в квадрат обеих частей уравнения приводится к квадратному [math]x^2+2x-8=0[/math] с корнями [math]x_1=-4,\;x_2=2.[/math] Корень [math]x_1=-4[/math] не удовлетворяет условию ОДЗ. Применяя определение логарифма ко второму уравнению, получаем квадратное уравнение [math]x^2-2x-8=0[/math] с корнями [math]x_1=-2;\;x_2=4.[/math]. Корень [math]x_1=-2[/math] не удовлетворяет условию ОДЗ. Таким образом исходное уравнение имеет 2 корня 2 и 4.
б) Сравним числа [math]2[/math] и [math]\log_35[/math]. [math]2=\log_39[/math] соответственно [math]2>\log_35[/math]
[math]4>2^\sqrt2[/math], т.к. [math]4=2^2,\;[/math] а [math]2>\sqrt2\;[/math]
Следовательно [math]2\in\left[\log_35;2^\sqrt2\right]\;[/math], a [math]4\not\in\left[\log_35;2^\sqrt2\right]\;[/math]
Ответ: а) 2,4 б) 2
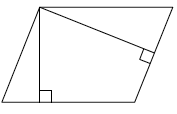
В правильной четырёхугольной пирамиде SABCD с вершиной S расстояние между прямыми BD и AS равно 2.
а) Постройте сечение пирамиды плоскостью, проходящей через точки А и S перпендикулярно прямой BD.
б) Найдите объём данной пирамиды, если её боковое ребро равно 5.
Решение:
а) Диагонали квадрата перпендикулярны, поэтому [math]\mathrm{AC}\perp\mathrm{BD}[/math] (см. рисунок) С другой стороны, так как пирамида правильная вершина [math]\mathrm S[/math] проецируется в центр основания, поэтому основание высоты и точка пересечения диагоналей квадрата [math]\mathrm{ABCD}[/math] совпадают. Обозначим эту точку [math]\mathrm O[/math], плоскость [math](\mathrm{SAO})\perp\mathrm{BD}[/math], так как содержит 2 пересекающиеся прямые, перпендикулярные BD. Сечение плоскостью [math]\mathrm{AOS}[/math] образует [math]\bigtriangleup SAC[/math], так как точки [math]A,O,C[/math] лежат на одной прямой.
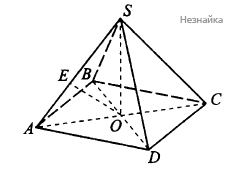
б) Обозначим через [math]O[/math] точку пересечения диагоналей квадрата. Диагональ [math]AC\perp BD[/math] и высота пирамиды [math]SO\perp BD[/math], поэтому [math]BD\perp AOS[/math]. Пусть [math]E[/math] - основание перпендикуляра, опущенного из точки [math]O[/math] на ребро SA. Так как [math]BD\perp AOS[/math], то [math]BD\perp OE[/math]
Таким образом, [math]OE[/math] - общий перпендикуляр к скрещивающимся прямым [math]BD[/math] и [math]SA[/math]. Заметим, что [math]OE[/math] - высота прямоугольного треугольника [math]AOS[/math], опущенная на гипотенузу [math]AS[/math]. Пусть [math]AO=a[/math] , тогда [math]SO=\sqrt{25-a^2}[/math]. Площадь треугольника [math]AOS[/math] равна [math]\frac12SA\times OE=5[/math], с другой стороны равна [math]\frac12AO\times SO=\frac12a\sqrt{25-a^2}[/math]. Решим уравнение [math]\frac12a\sqrt{25-a^2}=5[/math]. Оно имеет положительные корни [math]a=\sqrt5,\;a=2\sqrt5[/math]
Пусть [math]a=\sqrt5[/math], тогда [math]SO=2\sqrt5[/math] и площадь основания данной пирамиды равна [math]\frac12(2a)^2=10[/math]. Объем пирамиды [math]SABCD[/math] равен [math]\frac13\times10\times2\sqrt5=\frac{20\sqrt5}3[/math]
Пусть [math]a=2\sqrt5[/math], тогда [math]SO=\sqrt5[/math] и площадь основания данной пирамиды равна [math]\frac12(4\sqrt5)^2=40[/math]. Объем пирамиды [math]SABCD[/math] равен [math]\frac13\times40\times\sqrt5=\frac{40\sqrt5}3[/math]
Ответ: [math]\frac{20\sqrt5}3[/math] и [math]\frac{40\sqrt5}3[/math]
Решите неравенство [math]\left(x-1\right)\left(2\log_3^2x-5\log_3x+2\right)<0[/math].
Решение:
ОДЗ: [math]x>0[/math]
[math](x-1)(2\log_3^2x-5\log_3x+2)<0[/math]
[math](x-1)(\log_3x-2)(2\log_3x-1)<0[/math]
На ОДЗ выражение [math]\log_3x-2=\log_3x-\log_39[/math] совпадает по знаку с выражением [math]x-9[/math], а выражение [math]2\log_3x-1=2(\log_3x-\log_3\sqrt3)[/math] - с выражением [math]x-\sqrt3[/math]. Получим, что исходное неравенство на ОДЗ равносильно неравенству [math](x-1)(x-9)(x-\sqrt3)<0[/math]. Решив его методом интервалов получим [math]x\in(-\infty;1)\cup(\sqrt3;9)[/math]. Учитывая ОДЗ [math]x\in(0;1)\cup(\sqrt3;9)[/math]
Ответ: [math]\left(0;\;1\right)\cup\left(\sqrt3;\;9\right)[/math]
Внутри прямого угла АОВ проведён луч ОС. В угол ВОС вписана окружность, касающаяся лучей ОВ и ОС в точках B и C соответственно, в угол АОС вписана окружность, касающаяся лучей ОА и ОС в точках А и С соответственно. Радиус одной из этих окружностей в 4 раза больше радиуса другой.
а) Докажите, что ОА = ОВ.
б) Найдите косинус меньшего из углов АОС и ВОС.
Решение:
а) Не нарушая общности, можем считать, что большая окружность вписана в угол [math]AOC[/math]. Пусть [math]CQ=r;\;PC=4r[/math]. так как окружность с центром [math]P[/math] вписана в угол [math]AOC[/math], то [math]PA\perp OA,\;PC\perp OC,\;OA=OC[/math] как отрезки касательных, проведенные из одной точки. аналогично [math]OC=OB[/math], тогда [math]OA=OB[/math], что и требовалось доказать.
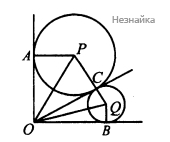
Из того, что [math]PO[/math] и [math]QO[/math] - биссектрисы углов [math]AOC[/math] и [math]BOC[/math] соответственно, следует, что [math]\angle POQ=45^\circ[/math]
Обозначим [math]OA=OB=OC=x[/math], тогда [math]OP=\sqrt{16r^2+x^2\;},\;OQ=\sqrt{r^2+x^2},\;PQ=4r+r=5r[/math]. Учитывая, что [math]\angle POQ=45^\circ,[/math] по теореме косинусов имеем [math]PQ^2=OP^2+OQ^2-2OP\times OQ\times\frac{\sqrt2}2[/math]
[math]16r^2+x^2+r^2+x^2-\sqrt2\sqrt{16r^2+x^2}\sqrt{r^2+x^2}=25r^2[/math], решая уравнение относительно [math]x^2[/math] , получим [math]x^2=\frac{33\pm5\sqrt{41}}2r^2[/math]
[math]\cos\angle COQ=\frac{OC}{OQ}=\frac x{\sqrt{r^2+x^2}}=\sqrt{\frac{33\pm5\sqrt{41}}{35\pm5\sqrt{41}}}.[/math]
Если [math]\cos\angle COQ=\sqrt{\frac{33-5\sqrt{41}}{35-5\sqrt{41}}}.[/math], то [math]\cos\angle BOC=\cos(2\angle COQ)=2\cos^2\angle COQ-1=2\times\frac{33-5\sqrt{41}}{35-5\sqrt{41}}-1=\frac{31-5\sqrt{41}}{35-5\sqrt{41}}<0[/math], что противоречит тому, что [math]\angle BOC<90^\circ[/math]
Если [math]\cos\angle COQ=\sqrt{\frac{33+5\sqrt{41}}{35+5\sqrt{41}}},[/math] то [math]\cos\angle BOC=\cos(2\angle COQ)=2\cos^2\angle COQ-1=2\times\frac{33+5\sqrt{41}}{35+5\sqrt{41}}-1=\frac{3+\sqrt{41}}{10}[/math]
Ответ: [math]\frac{3+\sqrt{41}}{10}[/math].
Молокозавод ежедневно отправляет в магазины 12000 литровых пакетов молока (равное количество в каждый магазин). Подсчитано, что в понедельник выгоднее в четыре магазина молоко не отправлять, а предназначенное для них молоко распределять (в равной мере) среди остальных магазинов. При этом каждый магазин увеличивает количество разливного молока на 800 пакетов (это их предельная продажа). Сколько пакетов молока составляет предельная продажа?
Решение:
Обозначим через [math]x[/math] количество магазинов, в которые молокозавод отправляет молоко. Тогда [math]\frac{12000}x[/math] пакетов молока реализуют магазины во все дни недели, кроме понедельника, а [math]\frac{12000}x+800[/math] в понедельник. По условию задачи в понедельник в четыре магазина молоко не отправляется , значит [math]\frac{12000}{x-4}[/math] пакетов отправляется в другие магазины по понедельникам. Составим и решим уравнение:
[math]\frac{12000}x+800=\frac{12000}{x-4},\;x>4[/math]
[math]x=10[/math]
[math]\frac{12000}{10-4}=2000[/math] пакетов молока составляет предельная продажа.
Ответ: 2000
При каких значения параметра а система [math]\left\{\begin{array}{l}y=x^2+8x-2,\\y=4a-2x\end{array}\right.[/math] имеет ровно одно решение на отрезке х ∈ [-6 ; 2]?
Решение:
Схематически изобразим график функции [math]y_1=x^2+8x-2[/math] при [math]x\in\left[-6;2\right][/math]. Это фрагмент параболы с вершиной (-4;-18). При этом [math]y_2=4a-2x[/math] - это семейство параллельных прямых. Очевидно, что искомые значения параметра принадлежат промежутку [math](a_1;a_2)\cup\left\{a_3\right\}[/math], если точка касания, соответствующая [math]a_3[/math], принадлежит отрезку [math]\left[-6;2\right][/math] и [math]a\in(a_1;a_2\rbrack[/math] в противном случае. Учитывая, что [math]y_1(-6)=-14;\;y_1(2)=18,\;[/math] определим координаты точек [math]A,B:\;A(-6;-14),\;B(2,18)\;[/math]
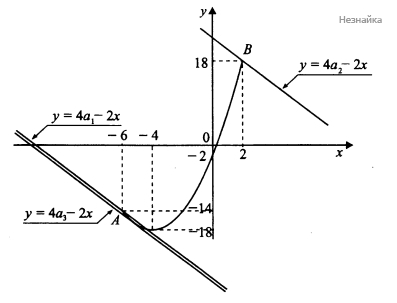
[math]\begin{array}{l}a_1:\;4a_1-2(-6)=-14;\;a_1=-\frac{13}2\\a_2:\;4a_2-2\times2=18;\;a_2=\frac{11}2\end{array}[/math]
Определим [math]a_3[/math]: уравнение [math]x^2+8x-2=4a-2x[/math] должно иметь единственное решение. Уравнение будет иметь единственное решение, когда дискриминант равен 0. [math]D=100+8+16a=0,\;a=-\frac{27}4[/math] в этом случае [math]x[/math] равен решению уравнения [math]x^2+10x+25=0[/math], то есть [math]x=-5\in\left[-6;2\right][/math]
Ответ: {-27/4}⋃(-13/2; 11/2]
Ежедневно в зоопарке каждой лисе полагается 2 кг мяса, тигру — 14 кг, льву — 21 кг. Известно, что у каждого льва бывает ежедневно 230 посетителей, у каждой лисы — 20, у каждого тигра — 160 и все эти звери есть в зоопарке.
а) Какое число посещений будет у этих животных, если ежедневно в зоопарке распределяют 70 кг мяса?
б) Может ли ежедневно распределяться 420 кг мяса, если известно, что посещений за 1 день было меньше 4000?
в) Каким может быть наибольшее ежедневное число посещений у этих зверей, если зоопарк ежедневно распределяет между ними 111 кг мяса?
Решение:
Обозначим число лис в зоопарке буквой c, львов - l, тигров - t. Тогда им ежедневно дают [math]2c+14t+21l[/math] кг мяса, а посетителей бывает [math]20c+160t+230l=P[/math]
а) По условию [math]2c+14t+21l=70[/math], где [math]\{c,t,l\}\subset\mathbb{Z}[/math]. 70 делится на 7 и [math]14t+21l[/math] делится на 7, значит 2с, а следовательно, и с делится на 7. Если [math]с=7[/math], то [math]14+7(2t+3l)=70[/math], [math]2t+3l=8[/math]. При [math]t\in\mathbb{N}\;l<\frac83[/math] и делится на 2, значит [math]l=2,t=1[/math] и число посетителей равно [math]20\times7+160\times1+230\times2=760[/math]
б) По условию, [math]2c+14t+21l=420[/math]. Может ли [math]20c+160]t+230l[/math] быть меньше 4000?
[math]20c+160t+230l=10(2c+16t+23l)>10(2c+14t+21l)=10\times420=4200[/math]. Получилось, что [math]20c+160t+230l>4200[/math], значит, при таких условиях не может ежедневно распределяться 420кг мяса
в) Нам дано, что [math]2c+14t+21l=111[/math]. Так как количество животных натуральные числа, [math]l[/math] нечетно и [math]21l\leq111-(2+14),\;[/math][math]21l\leq95,\;[/math][math]l\leq4,\;[/math] то есть [math]l=3[/math] или [math]l=1[/math]
1) [math]l=1[/math], тогда [math]2с+14t+21=111;[/math][math]2с+14t=90;[/math][math]с+7t=45;[/math][math]с=45-7t;[/math][math]t\leqslant6\frac27[/math]. Число посетителей:
[math]P=20c+160t+230l=20(45-7t)+160t+230=1130+20t[/math] наибольшее при наибольшем [math]t[/math], т.е.при [math]t=6[/math], [math]P=1130+20\times6=1250[/math].
2) [math]l=3[/math], тогда [math]2с+14t+21\times3=111;[/math][math]2с+14t=48;[/math][math]c=24-7t\geqslant1;[/math][math]t\leqslant3\frac27[/math]
[math]P=20c+160t+230\times3=20t+1170[/math] наибольшее при наибольшем [math]t[/math], т.е. при [math]t=3[/math]. [math]P=20\times3+1170=1230[/math]
Наибольшее число посетителей 1250.
Ответ: а) 760 б) не может в) 1250
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||