Вариант 11
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
На счету Сашиного мобильного телефона было 164 рубля, а после разговора с Таней осталось 84 рубля. Сколько минут длился разговор с Таней, если одна минута разговора стоит 2 рубля 50 копеек?
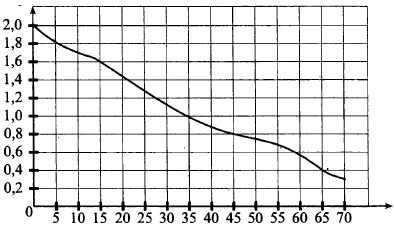
При работе фонарика батарейка постепенно разряжается, и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по рисунку, за сколько часов напряжение упадёт с 1,6 до 0,8 вольт.
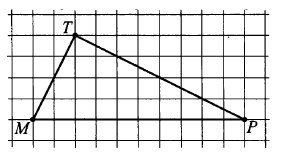
Найдите радиус окружности, описанной около прямоугольного треугольника РМТ, если стороны квадратных клеток равны 1 см.
Чтобы пройти в следующий круг соревнований, футбольной команде нужно набрать хотя бы 4 очка в двух играх. Если команда выигрывает, она получает 3 очка, в случае ничьей — 1 очко, если проигрывает — 0 очков.
Найдите вероятность того, что команде удастся выйти в следующий круг соревнований. Считайте, что в каждой игре вероятности выигрыша и проигрыша одинаковы и равны 0,2.
Найдите корень уравнения logx 25 = 2.
В треугольнике АВС угол С равен 90°, sin A = 0,3. Найдите cos В.
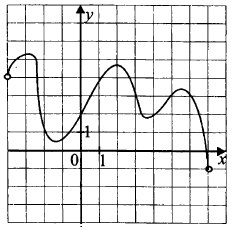
На рисунке изображён график функции у = f(x), определённой на интервале (—4; 7). Найдите количество точек, в которых касательная к графику функции параллельна прямой у = — 2 или совпадает с ней.
Конус объёмом 5,3 вписан в шар. Радиус основания конуса равен радиусу шара. Найдите объём шара.
Найдите значение выражения [math]15tg15^\circ\times tg285^\circ[/math]
Ёмкость высоковольтного конденсатора в телевизоре С = 3 • 10-6 Ф. Параллельно с конденсатором подключён резистор с сопротивлением R = 6 • 106 Ом. Во время работы телевизора напряжение на конденсаторе U0 = 24 кВ. После выключения телевизора напряжение на конденсаторе убывает до значения U (кВ) за время, определяемое выражением [math]t=\alpha RC\log_2\frac{U_0}U[/math] (с), где [math]\alpha[/math] = 1,5 — постоянная. Определите наибольшее возможное напряжение (в киловольтах) на конденсаторе, если после выключения телевизора прошло не менее 54 с.
В понедельник акции компании подешевели на некоторое число процентов, а во вторник подорожали на то же самое число процентов. В результате они стали стоить на 9% дешевле, чем при открытии торгов в понедельник. На сколько процентов подешевели акции компании в понедельник?
Найдите точку максимума функции [math]y=-\frac x{3969+x^2}[/math].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math](\sqrt{x^2+2x-7}-1)\log_3(9+2x-x^2)=0[/math]
б) Найдите все корни этого уравнения, принадлежащие промежутку [math]\left[\log_35;2^\sqrt2\right][/math].
Решение:
а) Данное уравнение определено при условиях [math]\left\{\begin{array}{l}x^2+2x-7\geq0\\9+2x-x^2>0\end{array}\right.[/math] и расщепляется на 2 уравнения [math]\sqrt{x^2+2x-7}-1=0[/math] и [math]\log_3(9+2x-x^2=0)[/math]. Первое уравнение после возведения в квадрат обеих частей уравнения приводится к квадратному [math]x^2+2x-8=0[/math] с корнями [math]x_1=-4,\;x_2=2.[/math] Корень [math]x_1=-4[/math] не удовлетворяет условию ОДЗ. Применяя определение логарифма ко второму уравнению, получаем квадратное уравнение [math]x^2-2x-8=0[/math] с корнями [math]x_1=-2;\;x_2=4.[/math]. Корень [math]x_1=-2[/math] не удовлетворяет условию ОДЗ. Таким образом исходное уравнение имеет 2 корня 2 и 4.
б) Сравним числа [math]2[/math] и [math]\log_35[/math]. [math]2=\log_39[/math] соответственно [math]2>\log_35[/math]
[math]4>2^\sqrt2[/math], т.к. [math]4=2^2,\;[/math] а [math]2>\sqrt2\;[/math]
Следовательно [math]2\in\left[\log_35;2^\sqrt2\right]\;[/math], a [math]4\not\in\left[\log_35;2^\sqrt2\right]\;[/math]
Ответ: а) 2, 4 б) 2
На ребре A1D1 единичного куба ABCDA1B1C1D1 взята точка К, А1К : KD1 =1 : 2.
а) Постройте сечение куба, проходящее через точку К и параллельное прямым C1D и B1D1.
б) Найдите площадь этого сечения.
Решение:
Сделаем чертеж:
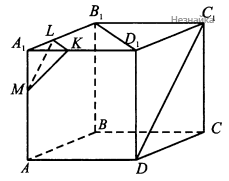
В плоскости [math]A_1B_1C_1[/math] через точку [math]K[/math] проведем [math]KL\parallel B_1D_1[/math]. в плоскости [math]AA_1B_1[/math] через точку [math]M[/math] проведем [math]LM\parallel C_1D[/math]. Соединим точку [math]M[/math] с точкой [math]K[/math]. Треугольник [math]MLK[/math] - искомое сечение.
б) По условию [math]A_1K:KD_1=1:2[/math], тогда [math]A_1K:A_1D_1=1:3[/math]. [math]\bigtriangleup LA_1K\sim\bigtriangleup B_1A_1D_1[/math] по 1 признаку подобия.
Из подобия следует, что [math]\frac{A_1L}{A_1B_1}=\frac{LK}{B_1D_1}=\frac{A_1K}{A_1D_1}=\frac13[/math]. [math]A_1B_1=A_1D_1[/math], Значит [math]A_1L=A_1K=\frac13[/math]. Аналогично [math]A_1M=A_1K=\frac13[/math] из [math]\bigtriangleup A_1LM[/math].
Имеем [math]A_1M=A_1K=A_1L=\frac13[/math]. Прямоугольные треугольники [math]A_1KL,\;A_1KM,\;A_1LM[/math] Равны по двум катетам, значит [math]KL=KM=LM=\frac{B_1D_1}3=\frac{\sqrt2}3[/math]. [math]S_{KLM}=\frac{KL^2\sqrt3}4=\frac{\sqrt3}{18}[/math]
Ответ: [math]\frac{\sqrt3}{18}[/math]
Решите неравенство [math]\left(x-1\right)\left(2\log_3^2x-5\log_3x+2\right)<0[/math].
Решение:
ОДЗ: [math]x>0[/math]
[math](x-1)(2\log_3^2x-5\log_3x+2)<0[/math]
[math](x-1)(\log_3x-2)(2\log_3x-1)<0[/math]
На ОДЗ выражение [math]\log_3x-2=\log_3x-\log_39[/math] совпадает по знаку с выражением [math]x-9[/math], а выражение [math]2\log_3x-1=2(\log_3x-\log_3\sqrt3)[/math] - с выражением [math]x-\sqrt3[/math]. Получим, что исходное неравенство на ОДЗ равносильно неравенству [math](x-1)(x-9)(x-\sqrt3)<0[/math]. Решив его методом интервалов получим [math]x\in(-\infty;1)\cup(\sqrt3;9)[/math]. Учитывая ОДЗ [math]x\in(0;1)\cup(\sqrt3;9)[/math]
Ответ: [math]\left(0;\;1\right)\cup\left(\sqrt3;\;9\right)[/math]
Внутри прямого угла АОВ проведён луч ОС. В угол ВОС вписана окружность, касающаяся лучей ОВ и ОС в точках В и С соответственно, в угол АОС вписана окружность, касающаяся лучей ОА и ОС в точках А и С соответственно. Радиус одной из этих окружностей в 3 раза больше радиуса другой.
а) Докажите, что если Р и Q — центры этих окружностей, то ∠POQ = 45°.
б) Найдите косинус меньшего из углов АОС и ВОС.
Решение:
а) Не нарушаю общности, можем считать, что большая окружность вписана в угол [math]AOC[/math]. Пусть [math]CQ=r,\;PC=3r[/math] (см. рисунок). Так как окружность с центром [math]P[/math] вписана в угол [math]AOC[/math] , то [math]PA\perp OA,\;PC\perp OC,\;OA=OC[/math] как отрезки касательных, проведенные из одной точки. Тогда [math]\bigtriangleup PAO=\bigtriangleup PCO[/math] и значит [math]\angle AOP=\angle COP[/math]. Аналогично [math]\angle COQ=\angle BOQ[/math]. Отсюда [math]\angle POQ=\angle POC+\angle QOC=\frac12\angle AOC+\frac12\angle BOC=\frac12\angle AOB=45^\circ[/math]. Тем самым доказано утверждение пункта а
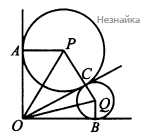
б) Обозначим [math]OA=OC=OB=x[/math]. Тогда [math]OP=\sqrt{9r^2+x^2}[/math], [math]OQ=\sqrt{r^2+x^2}[/math]. [math]PQ=3r+r=4r[/math]. Учитывая, что [math]\angle POQ=45^\circ[/math] по теореме косинусов [math]PQ^2=OP^2+OQ^2-2OP\times OQ\times\frac{\sqrt2}2[/math]
[math]9r^2+x^2+r^2+x^2-\sqrt2\sqrt{9r^2+x^2}\times\sqrt{r^2+x^2}=16r^2[/math]
[math]x^2=(11\pm4\sqrt7)r^2[/math]
[math]\cos\angle COQ=\frac{OC}{OQ}=\frac x{\sqrt{r^2+x^2}}=\sqrt{\frac{11\pm4\sqrt7}{12\pm4\sqrt7}}[/math]
Если [math]\cos\angle COQ=\sqrt{\frac{11-4\sqrt7}{12-4\sqrt7}}[/math], то [math]\cos\angle BOC=\cos(2\angle COQ)=\frac{5-2\sqrt7}{6-2\sqrt7}<0[/math], что противоречит тому, что [math]\angle BOC<90^\circ[/math]
Если [math]\cos\angle COQ=\sqrt{\frac{11+4\sqrt7}{12+4\sqrt7}}[/math], то [math]\cos\angle BOC=\cos(2\angle COQ)=\frac{1+\sqrt7}4[/math]
Ответ: [math]\frac{1+\sqrt7}4[/math].
Первоначально годовой фонд заработной платы столовой составлял 150 000 рублей. После увеличения числа клиентов, штатное расписание было увеличено на 9 человек, а фонд заработной платы возрос до 525 000 рублей, средняя годовая заработная плата (относительно всех сотрудников) стала больше на 10 000 рублей. Какова стала средняя заработная плата (относительно всех сотрудников) после увеличения годового фонда?
Решение:
Пусть изначально в столовой работали [math]n[/math] человек. Тогда средняя годовая заработная плата (в рублях) равнялась [math]\frac{150000}n[/math]. После увеличения числа клиентов штат сотрудников составил [math]n+9[/math] человек, а средняя годовая заработная плата возросла до [math]\frac{525000}{n+9}[/math] рублей. По условию [math]\frac{525000}{n+9}-\frac{150000}n=10000[/math] Найдем n.
[math]\begin{array}{l}\frac{105}{n+9}-\frac{30}n=2\\\frac{105n-30(n+9)}{n(n+9)}=\frac{75n-270}{n(n+9)}=2\\2n^2+18n=75n-270\\2n^2-57n+270=0\\n_1=6;\;n_2=22,5.\end{array}[/math]
Число сотрудников должно выражаться неотрицательным целым числом, поэтому [math]n=6[/math], тогда [math]n+9=15[/math]. Искомая средняя годовая заработная плата равна [math]\frac{525000}{15}=35000[/math] рублей.
Ответ: 35000 рублей.
Найдите все значения параметра a, при которых уравнение [math]\log_\frac1a(\sqrt{x^2+ax+10}+1)lg(x^2+ax+11)+2\log_a2=0[/math] имеет ровно одно решение.
Решение:
ОДЗ: [math]\left\{\begin{array}{l}\;\;\;\;\;\;\;\;\;a>0,\\\begin{array}{c}a\neq1,\\x^2+ax+10\geq0\\x^2+ax+11>0\end{array}\end{array}\right.[/math][math]\left\{\begin{array}{l}\;\;\;\;\;\;\;\;\;a>0,\\\begin{array}{c}a\neq1,\\x^2+ax+10\geq0\end{array}\end{array}\right.[/math]
Обозначим [math]x+\frac\alpha2=t.[/math]
Уравнение примет вид
[math]log_\frac1a(\sqrt{t^2+10-\frac{a^2}4}+1)lg(t^2+11-\frac{a^2}4)+2\log_a2=0.[/math]
Функция [math]f(t)=log_\frac1a(\sqrt{t^2+10-\frac{a^2}4}+1)lg(t^2+11-\frac{a^2}4)+2\log_a2[/math] - четная
Исходное уравнение имеет ровно одно решение при [math]t=0[/math], в противном случае будет иметь не менее двух решений,что противоречит условию задачи.
Имеем [math]f(0)=0.[/math]
[math]\log_\frac1a(\sqrt{10-\frac{a^2}4}+1)lg(11-\frac{a^2}4)+2\log_a2=0. (1)[/math]
Пусть [math]\sqrt{10-\frac{a^2}2}=b,\;b\geq0.[/math] Тогда уравнение (1) принимает вид: [math]\begin{array}{l}-\log_a(b+1)lg(b^2+1)+\log_a4=0,\\\log_2(b+1)\times log_2(b^2+1)=\log_24\times\log_210.\;(2)\end{array}[/math]
Если [math]b=0[/math], то получаем противоречие, поэтому [math]b>0,\;b+1>1[/math] и [math]b^2+1>1[/math]. Отсюда следует, что функции [math]g(b)=\log_2(b+1)[/math] и [math]f(b)=\log_2(b^2+1)[/math] являются возрастающими положительными функциями. Их произведение является тоже возрастающей функцией.
Если [math]b+1=4[/math] и [math]b^2+1=10[/math], то [math]b=3[/math] удовлетворяет (2).
Других решений уравнение (2) не имеет, так как права часть уравнения (2) является константой.
Ответ: [math]a=2[/math]
Натуральное число называется палиндромом, если при расстановке его цифр в обратном порядке оно не изменяется (например, 8, 22, 171 и т.п.).
а) Сколько существует пятизначных палиндромов?
б) Существует ли 2015-значное число, квадрат которого является палиндромом?
в) Сколько существует палиндромов, квадраты которых не превышают 100000 и так же являются палиндромами?
Решение:
а) Пятизначный палиндром имеет вид [math]xyzyx[/math], где [math]y,z[/math] - любые цифры, [math]x[/math] - любая цифра, кроме 0. Значит всего существует [math]9\times10\times10=900[/math] пятизначных палиндромов.
б) Да, приведем пример. Пусть [math]x=10^{2014}+1[/math] — 2015-значное число, тогда [math]x^2=10^{4028}+2\times10^{2014}+1=1\underbrace{000...000}2\underbrace{000...000}1[/math] - палиндром.
в)Обозначим исходный палиндром [math]A[/math]. Ясно, что [math]A[/math] - не более, чем трехзначное натуральное число, причем [math]A<317[/math] .
[math]317^2=100489>100000[/math]. Рассмотрим 3 случая.
1) [math]A[/math] - однозначное число. Перебором чисел от 1 до 9 определим, что лишь квадраты чисел 1;2 и 3 являлются палиндромами
2) Двузначные палиндромы: 11,22,33,44,55,66,77,88,99. Непосредственно убедимся, что только [math]11^2[/math] и [math]22^2[/math] являются палиндромами
3) Пусть A трехзначное число, меньшее 317, и [math]A=xyx[/math], тогда [math]1\leq x\leq3[/math] и [math]A^2=(100x+10y+x)^2=x^2\times10^4+2xy\times10^3+(2x^2+y^2)\times10^2\;+2xy\times10+x^2[/math]. Так как [math]1\leq x^2\leq9[/math] , то [math]x^2[/math] является первой и последней цифрой числа [math]A^2[/math]
Если [math]2xy\geq10[/math] , то вторая цифра [math]A^2[/math] ,будет больше [math]x^2[/math] и [math]A^2[/math] палиндромом не является. Поэтому [math]2xy<10[/math], если [math]A^2[/math] является палиндромом, у которого вторая и четверная цифры равны [math]2xy[/math].
Если [math]2x^2+y^2\geq10[/math], то вторая цифра [math]A^2[/math] ,будет больше [math]2xy[/math], поэтому [math]2x^2+y^2<10[/math].
Отсюда следует, что [math]2x^2<10[/math], значит [math]x=1[/math] или [math]x=2[/math]. Так как [math]2\leq2x^2[/math] и [math]2x^2+y^2<10[/math], то [math]y=0,1,2.[/math]
Получаем следующие числа: 101,11,121,202,212,222. Число 222 не удовлетворяет условию [math]2x^2+y^2<10[/math].
В этом случае 5 вариантов (101,111,121,202,212). Всего 10 возможных значений [math]A[/math]
Ответ: a) 900; б) да; в) 10.
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||