Вариант 10
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
На покраску одного м2 поверхности одним слоем расходуется 0,2 литра краски. Найдите, какое количество краски необходимо (в л), чтобы покрасить забор площадью 21 м2 в три слоя.
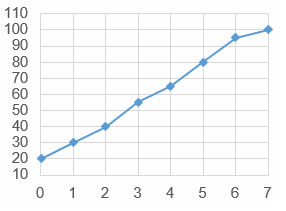
На рисунке представлен график нагревания некоторого количества воды. По горизонтали указано время (в мин.), прошедшее с момента начала нагревания, по вертикали — температура воды в соответствующее время (в °С). Определите по графику, за сколько минут температура воды выросла с 40 °C до 80 °С.
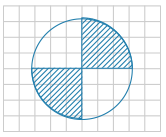
На клетчатой бумаге с размером клетки 1 см × 1 см изображена окружность. Вычислите площадь закрашенной фигуры в см2. В ответ укажите [math]\frac S\pi[/math].
В состязании по математике в команде «Незнайка в твоих штанах» 12 человек, из них три девочки. Отвечающего на вопрос члены жюри выбирают случайным образом. Найдите вероятность того, что выбранный участник — мальчик.
Решите уравнение [math]log_2(x^2+6x+9)=4[/math]. В ответе укажите меньший корень.
AD — основание равнобедренной трапеции ABCD. Диагонали трапеции пересекаются под прямым углом в точке O, угол A равен 75 °. Найдите длину боковой стороны (в см), если OD = [math]6\sqrt3[/math] см.
Изменение координаты точки выражается функцией [math]f(t)=\frac25\sqrt[2]{t^2}+\frac{t^2}2+6\sqrt t[/math], где t (в с) — время движения. Определите, какова была мгновенная скорость (в м/с) при t = 9 c.
Площадь полной поверхности цилиндра равна 628 см. Найдите объём вписанного в него конуса, если радиус основания равен 5 см. Число [math]\pi[/math] следует считать равным 3,14.
Найдите значение выражения [math]\frac{cos^2\left(\frac\pi2+x\right)}{1-sin^2x}-\frac1{cos^2x}[/math], если tg x = 1,6.
Для вычисления коэффициента эффективности миграции (в %) используется формула [math]K=\frac{P-B}{P+B}\cdot100[/math], где P — численность прибывших (в тыс. человек), B — численность выбывших (в тыс. человек). Сколько тысяч человек должно выехать из страны, чтобы коэффициент эффективности миграции достиг 10 % при 11 тыс. чел. прибывших?
Алексею необходимо выполнить грузоперевозку продукции массой 41,6 т. В первый день он перевез 200 кг товара. Найдите, на сколько тонн он ежедневно увеличивал массу привезённого товара по сравнению с предыдущим днём, если известно, что всю работу он выполнил за 13 дней.
Найдите точку минимума функции [math]f(x)=2^x-128x\;ln2[/math]
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
Дано уравнение [math]\sqrt{-ctgx}\cdot\left(2\cos^2x-\cos x-1\right)=0[/math].
А) Решите уравнение.
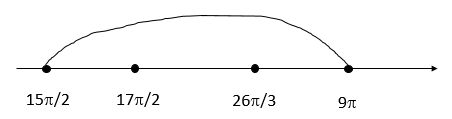
Б) Укажите его корни из промежутка [math]\left[\frac{15\pi}2;\;9\pi\right][/math].
А) ОДЗ: [math]sinx\neq0;ctgx<0[/math]
[math]\sqrt{-ctgx}=0[/math]
[math]cosx=0[/math]
[math]x=\frac\pi2+\pi n[/math], [math]n\in Z[/math]
[math]2cos^2x-cosx-1=0[/math]
[math]a=2;b=-1;c=-1;a+b+c=0\Rightarrow x_1=1;x_2=\frac ca[/math]
[math]\Rightarrow cosx=1;cosx=-\frac12[/math]
[math]x=2\pi n[/math] - не соответствует ОДЗ, [math]x=-\frac{2\pi}3+2\pi k;\;x=\frac{2\pi}3+2\pi k[/math], [math]k\in N[/math]
[math]x=-\frac{2\pi}3+2\pi k[/math] - не соответствует ОДЗ
Б) Нанесем на числовую прямую и определим, какие корни входят в промежуток:
А) [math]\frac{2\pi}3+2\pi n;\;\frac\pi2+\pi k,\;n,\;k\in Z[/math]
Б) [math]\frac{15\pi}2;\;\frac{17\pi}2;\;\frac{26\pi}3[/math]
Дана правильная треугольная призма ABCA1B1C1.
А) Докажите, что прямая В1С1 перпендикулярна линии пересечения плоскостей АВС1 и АСВ1.
Б) Найдите угол между плоскостями АВС1 и АСВ1, если известно, что АВ=2, АА1=2.
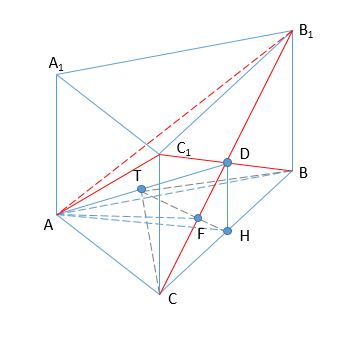
А) Доказать, что прямая В1С1 перпендикулярна линии пересечения плоскостей АВС1 и АСВ1.
т. [math]A\in(ABC_1)[/math]. т. [math]A\in(ACB_1)[/math]
[math]C_1B\in(ABC_1)[/math], [math]B_1C\in(ACB_1)[/math]
[math]C_1B\cap CB_1=D\Rightarrow D\in(ABC_1);D\in(ACB_1)[/math]
и [math]AD\in(ABC_1);AD\in(ACB_1)\Rightarrow AD[/math] - линия пересечения [math](ABC_1)[/math] и [math](ACB_1)[/math]
Имеем: необходимо доказать [math]B_1C_1\perp AD[/math]
Опустим из D перпендикуляр DH на CB ([math]DH\perp CB[/math])
т.D - не только высота треугольника, но и медиана,т.е.[math]CH=HB[/math]
т.к. [math]\bigtriangleup ABC[/math] - правильный, то AH - не только медиана, но и высота [math]\Rightarrow AH\perp CB[/math]
Тогда [math]AD\perp CB[/math] (по теореме о трех перпендикулярах)
А т.к. [math]CB\parallel C_1B_1[/math], то [math]AD\perp C_1B_1[/math], что и требовалось доказать
Б) [math]AB=2;AA_1=2;\angle((ABC_1);(ACB_1)-?[/math]
Опустим из C и B перпендикуляры на AD. Исходя из равенства [math]\bigtriangleup ADC=\bigtriangleup ADB[/math] (по трем сторонам) они упадут на одну точку, пусть т.Т
Имеем [math]CT\perp AD,BT\perp AD[/math], [math]\angle CTB[/math] - линейный угол искомого двугранного угла
[math]\bigtriangleup CTB[/math] - равносторонний [math]\Rightarrow TH\perp CB[/math]
Тогда [math]sin(\frac12\angle CTB)=\frac{HC}{CT}[/math]
Из [math]\bigtriangleup CHD[/math] по теореме Пифагора: [math]CD=\sqrt{CH^2+HD^2}[/math] ([math]HD=\frac12BB_1[/math]) [math]CD=\sqrt{1+1}=\sqrt2[/math]
Из [math]\bigtriangleup CHA[/math] по теореме Пифагора: [math]AH=\sqrt{AC^2-CH^2}[/math] [math]AH=\sqrt{4-1}=\sqrt3[/math]
Из [math]\bigtriangleup AHD[/math] по теореме Пифагора: [math]AD=\sqrt{AH^2+HD^2}[/math] [math]AH=\sqrt{3+1}=2[/math]
Имеем [math]AC=AD\Rightarrow\bigtriangleup CAD[/math] - равнобедренный . Опустим из А [math]AF\perp CD[/math]
При этом [math]CF=FD=\frac12CD=\frac{\sqrt2}2[/math]
Тогда из [math]\bigtriangleup AFC[/math] по теореме Пифагора [math]AF=\sqrt{AC^2-CF^2}=\sqrt{4-\frac12}=\sqrt{\frac72}[/math]
С одной стороны, [math]S_{\bigtriangleup ADC}=\frac12CT\cdot AD[/math], с другой стороны[math]S_{\bigtriangleup ADC}=\frac12AF\cdot CD\Rightarrow CT\cdot AD=AF\cdot CD\Rightarrow2CT=\sqrt{\frac72}\cdot\sqrt2\Rightarrow CT=\frac{\sqrt7}2[/math]
[math]sin(\frac12\angle CTB)=\frac1{\frac{\sqrt7}2}=\frac2{\sqrt7}\Rightarrow cos(\frac12\angle CTB)=\sqrt{1-\frac47}=\sqrt{\frac37}[/math], [math]sin(\angle((ABC_1);(ACB_1)))=2\cdot\frac2{\sqrt7}\cdot\sqrt{\frac37}=\frac{4\sqrt3}7[/math] и [math]cos(\angle((ABC_1);(ACB_1)))=\sqrt{1-\frac{16\cdot3}{49}}=\frac17[/math]
[math]\Rightarrow\angle((ABC_1);(ACB_1))=arccos(\frac17)[/math]
Ответ: [math]arccos\frac17[/math]
Решите неравенство [math]\log_{2+x}\frac13+\log_{2-x}3\leq0[/math].
ОДЗ: [math]2+x>0\Rightarrow x>-2; 2-x>0\Rightarrow x<2; 2+x\neq1; 2-x\neq1[/math]
[math]\frac{log_3\frac13}{log_3(2+x)}+\frac{log_33}{log_3(2-x)}\leq0[/math]
[math]-\frac1{log_3(2+x)}+\frac1{log_3(2-x)}\leq0[/math]
[math]\frac{-log_3(2-x)+log_3(2+x)}{log_3(2+x)\cdot log_3(2-x)}\leq0[/math]
Нули числителя: [math]log_3\frac{2+x}{2-x}=0[/math]
[math]\frac{2+x}{2-x}=1[/math]
[math]2+x=2-x[/math]
[math]x=0[/math]
Нули знаменателя: [math]log_3(2-x)=0\Rightarrow2-x=1\Rightarrow x=1[/math]
[math]log_3(2+x)=0\Rightarrow2+x=1\Rightarrow x=-1[/math]
Нанесем на числовую прямую нули числителя и знаменателя и расставим знаки:
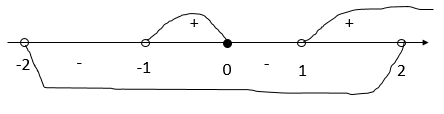
Ответ: (-1;0]⋃(1; 2)
В неравнобедренном треугольнике АВС ∠BAC = 45°. Продолжение биссектрисы CD треугольника пересекает описанную около него окружность υ1 в точке Е. Окружность υ2, описанная около треугольника ADE, пересекает продолжение стороны АС в точке F.
А) Докажите, что DE — биссектриса угла FDB.
Б) Найдите радиус окружности υ2, если известно, что АС=6, AF=2.
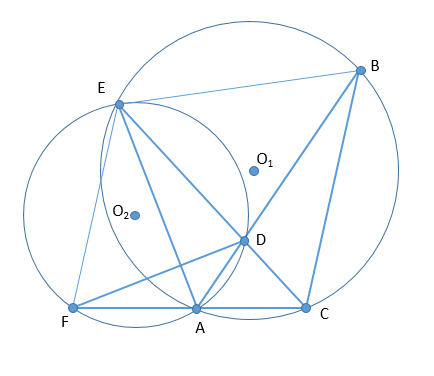
А) [math]\angle CEB=\angle BAC=45^\circ[/math] (опираются на одну и ту же дугу)
[math]\angle ABE=\angle ECA[/math] (опираются на одну и ту же дугу)
[math]\Rightarrow\angle EDB=180^\circ-\angle CEB-\angle ABE=180^\circ-45^\circ-\angle ECA=135^\circ-\angle ECA[/math]
[math]\angle ECB=\angle ECA[/math] (из условия)
Тогда [math]\angle EDB=\angle ECB+\angle CBD[/math] (как внешний) или[math]\angle EDB=\angle ECA+\angle CBD[/math]
[math]\angle AEC=\angle CBD[/math] (опираются на одну и ту же дугу)
[math]\angle AFD=\angle AED[/math] (опираются на одну и ту же дугу в окружности [math]v_2[/math])[math]\Rightarrow\angle AFD=\angle CBD[/math]
[math]\angle EDA=180^\circ-\angle EDB[/math] (как смежные)
Найдем [math]\angle FDE[/math]: [math]\angle FDE=\angle EDA-\angle FDA[/math];[math]\angle FDA=180^\circ-\angle FAD-\angle FDA[/math] (из [math]\bigtriangleup FAD[/math]), где [math]\angle DFA=\angle CBD[/math] (смотреть выше) и [math]\angle FAD=180^\circ-\angle DAC=180^\circ-45^\circ=135^\circ[/math] (как смежные)
[math]\Rightarrow\angle FDA=180^\circ-\angle CBD-45^\circ+\angle CBD=[/math][math]135^\circ-\angle EDB+\angle CBD=135^\circ-\angle ECA-\angle CBD+\angle CBD=[/math][math]135^\circ-\angle ECA=\angle EDB[/math]
Имеем, что [math]\angle FDE=\angle EDB\Rightarrow DE[/math] - биссектриса [math]\angle FDB[/math]
Б) Из [math]\bigtriangleup AFD[/math] по теореме синусов: [math]\frac{FD}{sin(\angle FAD)}=\frac{AF}{sin(\angle ADF)}=\frac{AD}{sin(\angle DFA)}=2R_{v_2}\Rightarrow\frac{AF}{sin(\angle ADF)}=R_{v_2}[/math]
[math]\frac2{sin(\angle ADF)}=2R_{v_2}\Rightarrow R_{v_2}=\frac1{sin(\angle ADF)}[/math]
[math]\bigtriangleup FDA=\bigtriangleup BDC[/math] (по стороне и двум прилежащим углам, CD - общая)
[math]\Rightarrow BC=FC;DC=AF+AC=2+6=8[/math]
Из [math]\bigtriangleup ABC[/math] по теореме синусов: [math]\frac{AC}{sin(\angle CBD)}=\frac{CB}{sin(\angle BAC)}=\frac{AB}{sin(\angle ACB)}=2R_{v_1}[/math][math]\Rightarrow\frac{AC}{sin(\angle CBD)}=\frac{CB}{sin(\angle BAC)}[/math]; [math]\Rightarrow\frac6{sin(\angle CBD)}=\frac{28}{\sqrt2}[/math][math]\Rightarrow sin(\angle CBD)=\frac{3\sqrt2}8[/math]
[math]\Rightarrow cos(\angle CBD)=\sqrt{1-\frac{9\cdot2}{64}}=\frac{\sqrt{48}}8[/math]
В пункте а) показывалось, что [math]\angle ADF=45^\circ-\angle CBD[/math]
[math]\Rightarrow sin(\angle ADF)=sin(45^\circ-\angle CBD)[/math][math]=sin(45^\circ)cos(\angle CBD)-cos(45^\circ)sin(\angle CBD)=\frac{\sqrt2}2\cdot\frac{\sqrt{46}}8-\frac{\sqrt2}2\cdot\frac{3\sqrt2}8[/math][math]=\frac{2\sqrt{23}-6}{2\cdot8}=\frac{\sqrt{23}-3}8[/math]
и [math]R_{v_2}=\frac8{\sqrt{23}-3}=\frac{8(\sqrt{23}+3)}{23-9}=\frac{24+8\sqrt{23}}{14}=\frac{12+4\sqrt{23}}7[/math]
Ответ: [math]\frac{12+4\sqrt{23}}7[/math]
В начале января 2017 года планируется взять кредит в банке на S млн. рублей, где S — целое число, на 4 года. Условия его возврата таковы:
- каждый июль долг возрастает на 10% по сравнению с началом текущего года;
- с августа по декабрь каждого года необходимо выплатить часть долга;
- в январе каждого года долг должен составлять часть кредита в соответствии со следующей таблицей:
| Начало года | 2017 | 2018 | 2019 | 2020 | 2021 |
| Долг (в млн. рублей) | S | 0,7S | 0,4S | 0,2S | 0 |
Найдите наибольшее значение S, при котором разность между наибольшей и наименьшей выплатами не будет превышать 2 млн. руб.
Найдем выплаты за каждый год и составим таблицу
| Год | 2017 | 2018 | 2019 | 2020 |
| Выплаты (в млн. рублей) | 1,1S-0,7S=0,4S | 1,1*0,7S-0,4S=0,37S | 1,1*0,4S-0,2S=0,24S | 1,1*0,2S-0S=0,22S |
Найдем наибольшее значение S, при котором разность между наибольшей и наименьшей выплатами не будет превышать 2 млн. руб. Для этого определим, что наибольшая выплата сделана в 2017г., а наименьшая- в 2020г. Получим следующее неравенство:
[math]0.4S-0.22S\leq2[/math]
[math]S\leq11.11[/math]
Следовательно, т.к. по условию S - целое число, то наибольшее значение S=11
Ответ: 11
Найдите все значения параметра а, при каждом из которых уравнение [math]2^{\sin x}+4\sin x+\sqrt{\sin x}+2=a\cdot\log_2\left(\frac{16}{1+\sin x}\right)[/math] не имеет корней.
Пусть [math]t=sinx[/math], [math]-1\leq t\leq1[/math]
[math]2^t+4t+\sqrt t+2=a\cdot log_2(\frac{16}{1+t})[/math], ОДЗ: [math]t\geq0\Rightarrow0\leq t\leq1[/math]
Рассмотрим на участке [math]t\in\lbrack0;1\rbrack[/math]:
[math]f(t)=2^t+4t+\sqrt t+2[/math] - монотонно возрастает при [math]t\in\lbrack0;1\rbrack[/math]
[math]f_{min}=f(0)=1+0+0+2=3[/math]
[math]f_{max}=f(1)=2+4+1+2=9[/math]
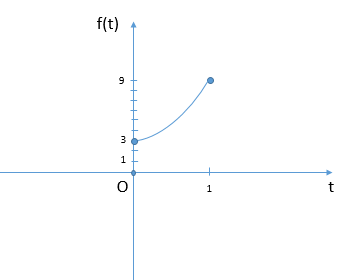
Рассмотрим [math]h(t)=alog_2\left(\frac{16}{1+t}\right)[/math] на участке [math]t\in\lbrack0;1\rbrack[/math]
При [math]a\geq0[/math] [math]h(t)[/math] неотрицательна при [math]t\in\lbrack0;1\rbrack[/math] и монотонно убывающая
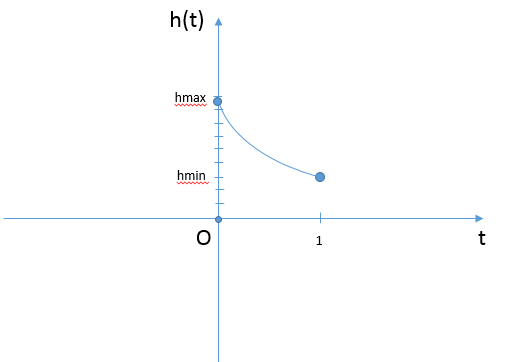
Тогда
[math]h_{min}=h(0)=alog_2\left(\frac{16}{1+0}\right)=4a[/math]
[math]h_{max}=h(1)=alog_2\left(\frac{16}{1+1}\right)=3a[/math]
При [math]a<0[/math] график [math]h(x)[/math] полностью лежит в нижней полуплоскости.
Рассмотрим уравнение при [math]a<0[/math], тогда графическое решение:
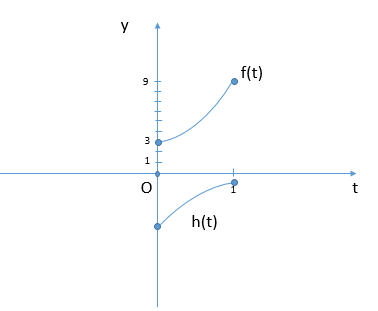
Откуда следует, что при [math]a<0[/math] уравнение не имеет решений!
Рассмотрим уравнение при [math]a\geq0[/math], тогда его графическое решение:
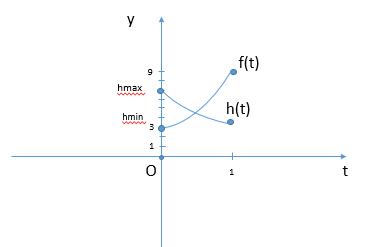
Откуда следует, что
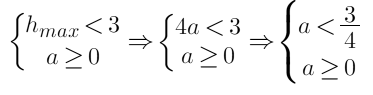
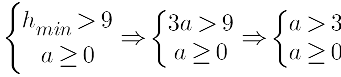
Объединение решений: [math]a\in(-\infty;\frac34)\cup(3;+\infty)[/math]
Ответ: (-∞; 0,75)⋃(3; +∞)
а) Найдите остаток от деления 20132014 на 5.
б) Найдите остаток от деления 20152016 на 3.
в) Найдите остаток от деления 20102011 на 17.
При решении задач учтем, что:
1) Ecли какое–то число a при делении на число b дает остаток d, то это можно записать в виде равенстваa=br+d, где r– частное, d– остаток
2) [math](A+\\\\\\\\\\\\\\\\alpha)^B=A\\\\\\\\\\\\\\\\cdot m+\\\\\\\\\\\\\\\\alpha^B[/math], где [math]\\\\\\\\\\\\\\\\alpha[/math] - малая величина по сравнению с А
А) [math]2013^{2014}=\\\\\\\\\\\\\\\\left(2010+3\\\\\\\\\\\\\\\\right)^{2014}=2010m+3^{2014}[/math]
[math]3^{2014}=9^{1007}=\\\\\\\\\\\\\\\\left(10-1\\\\\\\\\\\\\\\\right)^{1007}=10m-1^{1007}=10k+10-1=(10k+5)+4[/math], следовательно [math]d=4[/math]
Б) [math]2015^{2016}=\\\\\\\\\\\\\\\\left(2013+2\\\\\\\\\\\\\\\\right)^{2016}=\\\\\\\\\\\\\\\\left(671*3+2\\\\\\\\\\\\\\\\right)^{2016}=3m+2^{2016}[/math]
[math]2^{2016}=4^{1008}=\\\\\\\\\\\\\\\\left(3+1\\\\\\\\\\\\\\\\right)^{1008}=10m-1^{1007}=3k+1[/math], следовательно [math]d=1[/math]
В) [math]2010^{2011}=\\\\\\\\\\\\\\\\left(118*17+4\\\\\\\\\\\\\\\\right)^{2011}=17m+4^{2011}[/math]
[math]4^{2011}=4*\\\\\\\\\\\\\\\\left(16\\\\\\\\\\\\\\\\right)^{1005}=4*\\\\\\\\\\\\\\\\left(17-1\\\\\\\\\\\\\\\\right)^{1005}=4(17m-1^{1007})=17k+64[/math], следовательно [math]d=13[/math] ( остаток от деления 64 на 17)
\\\\n
Ответ: а) 4; б) 1; в) 13
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||