Задание № 8263
Радиусы двух окружностей с центрами О1 и О2, касающихся внешним образом в точке А, равны 6 и 3 соответственно. Их общая секущая, проведённая через точку А, пересекает первую окружность в точке В, вторую — в точке С.
а) Докажите, что [math]\frac{AB}{BC}=\frac{AO_1}{O_1O_2}[/math].
б) Найдите длину касательной, проведённой из точки В ко второй окружности, если дополнительно известно, что АВ = 4.
Решение:
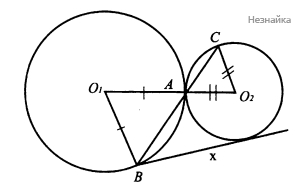
а) Рассмотрим случай, когда прямые [math]O_1O_2[/math] и [math]BC[/math] не совпадают (см. рисунок). Тогда [math]\bigtriangleup AO_1B[/math] и [math]\bigtriangleup AO_2C[/math] - равнобедренные ([math]AO_1=BO_1;\;AO_2=CO_2[/math] как радиусы), и, следовательно, [math]\angle O_1AB=\angle O_1BA[/math], [math]\angle O_2CA=\angle O_2AC[/math]. Но тогда [math]\bigtriangleup AO_1B\sim\bigtriangleup AO_2C[/math] по двум углам.
[math]\frac{BC}{AB}=\frac{AB+AC}{AB}=1+\frac{AC}{AB}[/math], но [math]\frac{AC}{AB}=\frac{AO_2}{AO_1}[/math], так как [math]\bigtriangleup ABO_1\sim\bigtriangleup ACO_2[/math]
Поэтому [math]\frac{BC}{AB}=1+\frac{AO_2}{AO_1}[/math]
С другой стороны [math]\frac{O_1O_2}{AO_1}=\frac{AO_1+AO_2}{AO_1}=1+\frac{AO_2}{AO_1}[/math]
Итак, [math]\frac{BC}{AB}=\frac{O_1O_2}{AO_1}[/math] (см. рисунок)
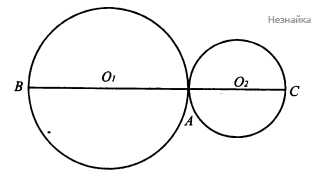
В случае, когда прямые [math]O_1O_2[/math] и [math]BC[/math] совпадают [math]\frac{AB}{BC}=\frac{2AO_1}{2AO_1+2AO_2}=\frac{AO_1}{AO_1+AO_2}=\frac{AO_1}{O_1O_2}[/math] (см. рисунок)
б) Обозначим x - искомая длина касательной, тогда
[math]\begin{array}{l}x^2=AB\times BC=AB^2\times\frac{O_1O_2}{AO_1}=16\times\frac96=24\\x=\sqrt{24}=2\sqrt6\\\end{array}[/math]
Ответ: [math]2\sqrt6[/math]
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.