Решение:

а) [math]\begin{array}{l}\cos3x=\cos(2x+x)=\cos2x\cos x-\sin2x\sin x=\\=(\cos^2x-\sin^2x)\cos x-2\sin^2\cos x=\\=(2\cos^2x-1)\cos x-2\cos x(1-\cos^2x)=4\cos^3-3\cos x\end{array}[/math]

Тогда исходное уравнение равносильно уравнению

[math]\begin{array}{l}4\cos^3-3\cos x=-2\cos x\\\cos x(4\cos^2x-1)=0\\\cos x=0;\;\;x=\frac{\mathrm\pi}2+\mathrm{πn},\;\mathrm n\in\mathbb{Z}\\\mathrm{cosx}=\pm\frac12;\;\mathrm x=\pm\frac{\mathrm\pi}3+\mathrm{πk},\;\mathrm k\in\mathbb{Z}\end{array}[/math]

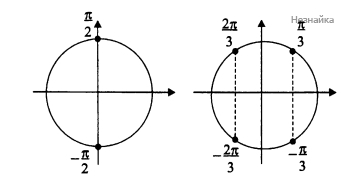
б) С помощью числовой окружности отберем корни, принадлежащие указанному промежутку:

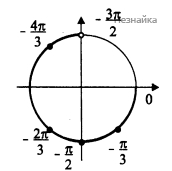
Ответ: а) [math]\frac{\mathrm\pi}2+\mathrm{πn},\;\mathrm n\in\mathbb{Z};[/math]

[math]\pm\frac{\mathrm\pi}3+\mathrm{πk},\;\mathrm k\in\mathbb{Z};[/math]

б) [math]-\frac{4\mathrm\pi}3,\;-\frac{2\mathrm\pi}3,\;-\frac{\mathrm\pi}2,\;-\frac{\mathrm\pi}3[/math]