Решение:

Сделаем замену [math]25^{-x}=t,\;t>0[/math]. Нам нужно, чтобы уравнение [math]at-a=2-\frac{t^2}5[/math] имело 2 корня, при этом [math]t_1=25^{-x_1}\leq25^{-\frac12}=\frac15[/math] [math]00[/math]

[math]a(t-1)=\frac{10-t^2}5,\;t=1[/math] - не является корнем

Рассмотрим функцию [math]y=a(t)=\frac{10-t^2}{5(t-1)}[/math] [math]y`(t)=\frac{t^2-2t+10}{-5(t-1)^2}[/math]

[math]y`(t)<0[/math] при всех допустимых значениях t, значит [math]y(t)[/math] убывает на [math](-\infty;1)\cup(1;+\infty)[/math]. [math]y(0)=-2;\;[/math] [math]y(\frac15)=-2,49;\;[/math]

Построим график (см. рисунок). По рисунку видно, что при [math]a\in(-2;-2,49\rbrack\;[/math] уравнение имеет 2 корня, один из которых [math]00[/math].

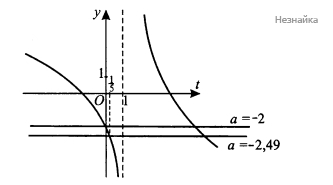
Ответ: [math]\lbrack-2,49;-2)[/math]