Вариант 16
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Плитка шоколада стоит 124 рубля. В понедельник в супермаркете действует специальное предложение: заплатив за две плитки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 680 рублей в понедельник?
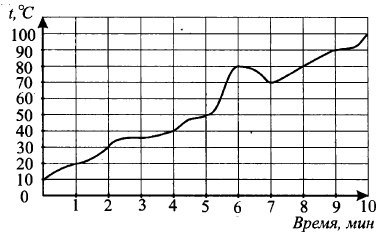
На графике показан процесс нагревания некоторого прибора. На оси абсцисс откладывается время в минутах, прошедшее с момента включения прибора, на оси ординат — температура прибора в градусах Цельсия. Определите по рисунку, за сколько минут прибор нагреется от 20° С до 50° С.
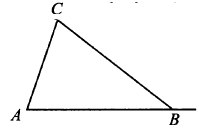
В треугольнике АВС АВ = ВС. Внешний угол при вершине В равен 142°. Найдите угол С. Ответ дайте в градусах.
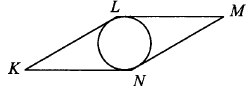
В волейбольной секции 26 человек, среди них два друга — Иван и Николай. На тренировке всех участников случайным образом делят на две группы по 13 человек в каждой. Найдите вероятность того, что Иван и Николай окажутся в одной группе.
Найдите корень уравнения
[math]\sqrt[3]{x-7}=-2[/math]
Острый угол ромба равен 30°. Радиус вписанной в этот ромб окружности равен 3,5. Найдите сторону ромба.
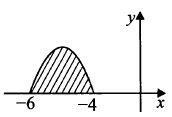
На рисунке 87 изображён график некоторой функции у = f(x). Функция [math]F\left(x\right)=-\frac23x^3-10x^2-48x+19[/math] — одна из первообразных функции f{x). Найдите площадь S закрашенной фигуры. В ответе укажите величину 3S.
Сосуд в форме цилиндра заполнен водой до отметки 36 см. Найдите, на какой высоте будет находиться уровень воды, если её перелить в другой сосуд в форме цилиндра, радиус основания которого в 3 раза меньше радиуса основания первого цилиндра. Ответ дайте в сантиметрах.
Найдите значение выражения (1 - log714)(1 - log214).
Рейтинг R интернет-магазина вычисляется по формуле
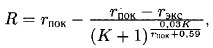
где rпок — средняя оценка магазина покупателями (от 0 до 1), rэкс — оценка магазина экспертами (от 0 до 0,7) и К — число покупателей, оценивших магазин.
Найдите рейтинг интернет-магазина «Альфа», если число покупателей, оставивших отзыв о магазине, равно 24, их средняя оценка равна 0,85, а оценка экспертов равна 0,1.
По двум параллельным железнодорожным путям в одном направлении следуют товарный и пассажирский поезда, скорости которых равны соответственно 75 км/ч и 60 км/ч. Длина пассажирского поезда равна 1000 м. Найдите длину товарного поезда, если время, за которое он прошёл мимо пассажирского поезда, равно 9 минутам. Ответ дайте в метрах.
Найдите точку минимума функции [math]y=(x+17)e^{x-12}[/math]
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math]\left(\frac65\right)^{\cos3x}+\left(\frac56\right)^{\cos3x}=2[/math].
б) Найдите все корни этого уравнения, принадлежащие промежутку [4π; 9π/2).
Решение:
а) [math]\left(\frac65\right)^{\cos3x}+\left(\frac65\right)^{-\cos3x}=2[/math]
Пусть [math]\left(\frac65\right)^{\cos3x}=a;[/math] [math]a+\frac1a=2;[/math] [math]a^2-2a+1=0;[/math][math]a=1.[/math]
[math]\left(\frac65\right)^{\cos3x}=1;[/math][math]\cos3x=0;[/math]
[math]x=\frac{\mathrm\pi}6+\frac{\mathrm{πn}}3;[/math]
б) [math]n=12;\;x=\frac{25\mathrm\pi}6[/math]
Ответ:
а) [math]\frac{\mathrm\pi}6+\frac{\mathrm{πn}}3,\;n\in\mathbb{Z};[/math]
б) [math]\frac{25\mathrm\pi}6[/math]
Косинус угла между боковыми гранями правильной треугольной пирамиды равен —1/8, сторона основания равна 12.
а) Постройте сечение этой пирамиды плоскостью, проходящей через сторону основания и перпендикулярную скрещивающемуся с ней ребру.
б) Найдите объём этой пирамиды.
Решение:
Рассмотрим пирамиду [math]MABC[/math], [math]AB=AC=BC=12[/math]. Проведем [math]AT\perp MB[/math], тогда [math]CT\perp MB[/math] (см. рисунок )
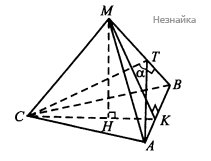
Докажем, это рассмотрев треугольники [math]CTB[/math] и [math]ATB[/math]. [math]TB[/math] - общая сторона, [math]CB=AB[/math], [math]\angle TBA=\angle TBC[/math].
[math]\bigtriangleup CTB=\bigtriangleup ATB[/math] по двум сторонам и углу между ними., поэтому [math]CT=AT[/math] и [math]\angle CTB=\angle ATB=90^\circ[/math]. Значит, [math]CAT[/math] - искомое сечение.
[math]\bigtriangleup CAT[/math] равнобедренный, пусть [math]CT=AT=x,\;\angle CTA=\alpha[/math] (угол между боковыми гранями)
По теореме косинусов [math]AC^2=x^2+x^2-2x^2\cos\alpha[/math]; [math]12^2=2x^2(1-\cos\alpha);[/math][math]x=8[/math]
Рассмотрим [math]\bigtriangleup ABM[/math]. В нем[math]AM=MB[/math] и [math]\sin\angle MBA=\frac{TA}{AB}=\frac8{12}=\frac23[/math]. Найдем высоту треугольника [math]\bigtriangleup ABM[/math], [math]MK\perp AB[/math]. [math]AK=KB=6[/math]
[math]\frac{MK}{KB}=tg\angle MBA=\frac2{\sqrt5}[/math], [math]MK=\frac2{\sqrt5}\times6=\frac{12}{\sqrt5}[/math]
Найдем высоту пирамиды [math]MH[/math] из [math]\bigtriangleup CMK[/math], в котором [math]CK=\frac{AC\sqrt3}2[/math] как высота правильного треугольника [math]ABC[/math], [math]H[/math] делит [math]CK[/math] в отношении [math]CH:HK=2:1.[/math]
[math]CK=\frac{12\sqrt3}2=6\sqrt3;[/math] [math]HK=\frac13CK=2\sqrt3[/math]
[math]MH^2=MK^2-HK^2=\left(\frac{12}{\sqrt5}\right)^2-\left(2\sqrt3\right)^2=\frac{84}5[/math]. [math]MH=\sqrt{\frac{84}5}=\frac{2\sqrt{21}}{\sqrt5}.[/math]
[math]S_{ABC}=\frac{AB^2\sqrt3}4=36\sqrt3[/math]
[math]V_{ABCM}=\frac13S_{ABC}\times MH=\frac13\times36\sqrt3\times\frac{2\sqrt{21}}{\sqrt5}=\frac{72\sqrt{35}}5[/math]
Ответ: [math]\frac{72\sqrt{35}}5[/math]
Решите систему неравенств
[math]\left\{\begin{array}{l}\left(x^2-9\right)\log_{x+8}\left(2-x\right)\leqslant0,\\48\cdot21^x+3\geqslant3^x+144\cdot7^x.\end{array}\right.[/math]
Решим первое неравенство системы методом рационализации.
ОДЗ [math]\left\{\begin{array}{l}\begin{array}{c}x+8>0\\x+8\neq0\end{array}\\2-x>0\end{array}\right.\left\{\begin{array}{l}\begin{array}{c}x>-8\\x\neq-7\end{array}\\x<2\end{array}\right.x\in(-8;-7)\cup(-7;2)[/math]
[math]\begin{array}{l}(x-3)(x+3)(x+8-1)(2-x-1)\leq0\\(x-3)(x+3)(x+7)(1-x)\leq0\end{array}[/math]
См. Рисунок 
Учитывая ОДЗ, [math]x\in(-8;-7)\cup\lbrack-3;1\rbrack[/math]
Решим второе неравенство:
[math]\begin{array}{l}3^x(48\times7^x-1)-3(48\times7^x-1)\geq0\\(3^x-3)(48\times7^x-1)\geq0\\3^x-3=0;\;x=1\\48\times7-1=0;\;x=-\log_748\end{array}[/math]
Заметим, что [math]-2\leq-\log_748\leq-1[/math]
[math]x\in(-\infty;-\log_748\rbrack\cup\lbrack1;+\infty)[/math]
Ответ: [math]\left(-8;\;-7\right)\cup\left[-3;\;-\log_748\right]\cup\left\{1\right\}[/math]
На сторонах АВ, ВС и АС треугольника АВС лежат точки М, Р и R соответственно, причём отрезки BR, СМ и АР пересекаются в точке О.
а) Докажите, что [math]\frac{AM}{MB}\cdot\frac{BP}{PC}\cdot\frac{CR}{RA}=1.[/math]
б) Найдите длину стороны АВ, если ВС = 10, АС = 13, ВМ : ВР = 3 : 2, CR = 9.
Решение:
Проведем из точек [math]A[/math] и [math]C[/math] перпендикуляры к прямой [math]BR[/math], тогда [math]CK\parallel AL[/math] (см. рисунок )
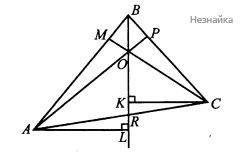
[math]\bigtriangleup ARL\sim\bigtriangleup CRK[/math], значит [math]\frac{AL}{CK}=\frac{AR}{RC}[/math]
[math]\frac{S_{AOB}}{S_{COB}}=\frac{0,5OB\times AL}{0,5OB\times CK}=\frac{AR}{RC}[/math]; [math]\frac{S_{COB}}{S_{AOB}}=\frac{RC}{AR}[/math]
Аналогично доказывается, что [math]\frac{S_{AOC}}{S_{BOC}}=\frac{AM}{MB}[/math] и [math]\frac{S_{BOA}}{S_{COA}}=\frac{BP}{PC}[/math]. Перемножим пропорции:
[math]\frac{S_{COB}}{S_{AOB}}\times\frac{S_{BOA}}{S_{COA}}\times\frac{S_{AOC}}{S_{BOC}}=\frac{CR}{RA}\times\frac{AM}{MB}\times\frac{BP}{PC}=1[/math]
б) [math]AC=13;[/math][math]CR=6,5;[/math][math]AR=13-6,5=6,5;[/math] [math]\frac{CR}{AR}=1;[/math] [math]\frac{BM}{BP}=\frac32;[/math][math]BM=1,5BP;[/math]; [math]1\times\frac{AM}{1,5BP}\times\frac{BP}{PC}=1;[/math] [math]AM=1,5PC[/math]
[math]AB=BM+AM=1,5BP+1,5PC=1,5(BP+PC)=1,5BC=15[/math]
Ответ: 15
Цена производителя на товар Б составляет 40 рублей. Прежде чем попасть на прилавок магазина, товар проходит через несколько фирм-посредников, каждая из которых увеличивает текущую цену в 2 или 3 раза и осуществляют услуги по транспортировке и хранению товара. Магазин делает наценку 15%, после чего покупатель приобрёл товар за 828 рублей. Сколько посредников было между магазином и производителем?
Решение:
Определим цену, по которой магазин закупил товар Б у посредника. Она равна 828:1,15=720 рублей. Значит, за счет посредников цена возросла в [math]\frac{720}{40}=18[/math] раз. Пусть [math]k[/math] посредников увеличивали цену в 2 раза, [math]m[/math] в 3 раза. Тогда [math]18=2^k\times3^m[/math], 2 и 3 - взаимно простые числа. Но [math]18=2^1\times3^2[/math], поэтому [math]k=1,\;m=2[/math]. Общее число посредников равняется [math]k+m=1+2=3[/math].
Ответ: 3
Найдите все значения параметра а, при каждом из которых уравнение [math]\frac a{25^x}-a=2-\frac{25^{-2x}}5[/math] имеет ровно 2 корня, хотя бы один из которых не менее 0,5.
Решение:
Сделаем замену [math]25^{-x}=t,\;t>0[/math]. Нам нужно, чтобы уравнение [math]at-a=2-\frac{t^2}5[/math] имело 2 корня, при этом [math]t_1=25^{-x_1}\leq25^{-\frac12}=\frac15[/math] [math]00[/math]
[math]a(t-1)=\frac{10-t^2}5,\;t=1[/math] - не является корнем
Рассмотрим функцию [math]y=a(t)=\frac{10-t^2}{5(t-1)}[/math] [math]y`(t)=\frac{t^2-2t+10}{-5(t-1)^2}[/math]
[math]y`(t)<0[/math] при всех допустимых значениях t, значит [math]y(t)[/math] убывает на [math](-\infty;1)\cup(1;+\infty)[/math]. [math]y(0)=-2;\;[/math] [math]y(\frac15)=-2,49;\;[/math]
Построим график (см. рисунок). По рисунку видно, что при [math]a\in(-2;-2,49\rbrack\;[/math] уравнение имеет 2 корня, один из которых [math]00[/math].
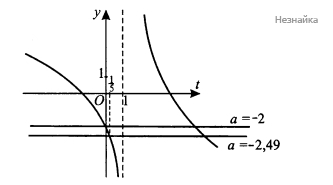
Ответ: [math]\lbrack-2,49;-2)[/math]
В океанариуме каждой акуле дают по 2,5 кг рыбы, мурене — 0,2 кг, скату — 1,5 кг ежедневно. Известно, что в среднем у каждой акулы бывает ежедневно 260 посетителей, у каждой мурены — 21, у каждого ската — 150. Все эти животные есть в океанариуме.
а) Какое число посещений будет у этих животных, если ежедневно в океанариуме им дают 6,5 кг рыбы?
б) Может ли ежедневно распределяться 18,4 кг рыбы, если известно, что за 1 день у этих животных было больше 2000 посещений?
в) Каким может быть наибольшее ежедневное число посещений, если океанариум ежедневно распределяет между ними 7 кг рыбы?
Решение:
Обозначим за a число акул, за с - число скатов, за m - число мурен в океанариуме. Тогда им ежедневно дают [math]2,5a+0,2m+1,5c[/math] кг рыбы и у них бывает в день [math]260a+21m+150c[/math] посетителей.
а) По условию [math]2,5a+0,2m+1,5c=6,5[/math] [math]\{a,m,c\}\subset\mathbb{N}[/math]
[math]25a+2m+15c=65;\;[/math] [math]2m=5(13-5a-3c).\;[/math] [math]m.\;[/math] делится на 5 и, так как [math]a\geq1,c\geq1[/math], [math]13-5a-3c\leq5[/math], [math]2m\leq25;\;m\leq12[/math]. Значит, m=5 или m=10.
[math]m=5[/math], тогда [math]25a+2\times5+15c=65;\;[/math][math]5a+3c=11;\;[/math] [math]a=1,c=2[/math]
Число посещений равно [math]260\times1+21\times5+150\times2=665.[/math]
[math]m=10,\;[/math] тогда [math]25a+2\times10+15c=65;\;[/math][math]5a+3c=9;\;[/math], [math]a=1;\;3c=4,\;c\not\in\mathbb{N}[/math]
б) Пусть [math]2,5a+0,2m+1,5c=18,4[/math] или [math]25a+2m+15c=184[/math]. Число посетителей в день
[math]P=260a+21m+150c=\frac{21}2(\frac{260\times2a}{21}+2m+\frac{150\times2c}{21})=[/math][math]=\frac{21}2(\frac{520a}{21}+2m+\frac{100c}7)<\frac{21}2(25a+2m+15c)=\frac{21}2\times184=1932[/math]
Получили, что [math]P<1932,\;[/math] значит не могло быть больше 2000 посещений.
в) По условию [math]2,5a+0,2m+1,5c=7[/math], то есть [math]25a=70-2m-15c[/math]; [math]25a\leq53[/math], то есть [math]a=1[/math] или [math]a=2[/math]
1) [math]a=1;\;[/math] [math]25+2m+15c=70;\;[/math] [math]2m+15c=45;\;[/math][math]15c=45-2m\geq15;\;[/math][math]m\leq15;\;[/math]
Число посетителей:
[math]P=260a+21m+150c=710+m[/math] наибольшее при наибольшем [math]m[/math]. [math]P=710+15=725[/math]
2) [math]a=2[/math]; [math]25\times2+2m+15c=70;\;[/math] [math]2m+15c=20;\;[/math][math]15c=20-2m\geq15;\;[/math] [math]m\leq2,5[/math]
[math]P=260a+21m+150c=260\times2+21m+10(20-2m)=720+m[/math]
[math]P[/math] наибольшее при значении [math]m[/math] наибольшем, то есть [math]m=2,[/math] [math]P=720+2=722[/math]
Наибольшее число посещений 725
Ответ: а) 665 б) не может в) 725
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||