Решение:

Рассмотрим пирамиду [math]MABC[/math], [math]AB=AC=BC=12[/math]. Проведем [math]AT\perp MB[/math], тогда [math]CT\perp MB[/math] (см. рисунок )

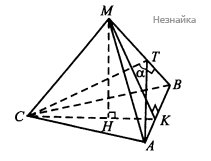
Докажем, это рассмотрев треугольники [math]CTB[/math] и [math]ATB[/math]. [math]TB[/math] - общая сторона, [math]CB=AB[/math], [math]\angle TBA=\angle TBC[/math].

[math]\bigtriangleup CTB=\bigtriangleup ATB[/math] по двум сторонам и углу между ними., поэтому [math]CT=AT[/math] и [math]\angle CTB=\angle ATB=90^\circ[/math]. Значит, [math]CAT[/math] - искомое сечение.

[math]\bigtriangleup CAT[/math] равнобедренный, пусть [math]CT=AT=x,\;\angle CTA=\alpha[/math] (угол между боковыми гранями)

По теореме косинусов [math]AC^2=x^2+x^2-2x^2\cos\alpha[/math]; [math]12^2=2x^2(1-\cos\alpha);[/math][math]x=8[/math]

Рассмотрим [math]\bigtriangleup ABM[/math]. В нем[math]AM=MB[/math] и [math]\sin\angle MBA=\frac{TA}{AB}=\frac8{12}=\frac23[/math]. Найдем высоту треугольника [math]\bigtriangleup ABM[/math], [math]MK\perp AB[/math]. [math]AK=KB=6[/math]

[math]\frac{MK}{KB}=tg\angle MBA=\frac2{\sqrt5}[/math], [math]MK=\frac2{\sqrt5}\times6=\frac{12}{\sqrt5}[/math]

Найдем высоту пирамиды [math]MH[/math] из [math]\bigtriangleup CMK[/math], в котором [math]CK=\frac{AC\sqrt3}2[/math] как высота правильного треугольника [math]ABC[/math], [math]H[/math] делит [math]CK[/math] в отношении [math]CH:HK=2:1.[/math]

[math]CK=\frac{12\sqrt3}2=6\sqrt3;[/math] [math]HK=\frac13CK=2\sqrt3[/math]

[math]MH^2=MK^2-HK^2=\left(\frac{12}{\sqrt5}\right)^2-\left(2\sqrt3\right)^2=\frac{84}5[/math]. [math]MH=\sqrt{\frac{84}5}=\frac{2\sqrt{21}}{\sqrt5}.[/math]

[math]S_{ABC}=\frac{AB^2\sqrt3}4=36\sqrt3[/math]

[math]V_{ABCM}=\frac13S_{ABC}\times MH=\frac13\times36\sqrt3\times\frac{2\sqrt{21}}{\sqrt5}=\frac{72\sqrt{35}}5[/math]

Ответ: [math]\frac{72\sqrt{35}}5[/math]