Решение:

а) В треугольнике [math]ABC\;AH\perp BC[/math], через точку [math]K[/math] проводим [math]KM\parallel AH[/math], отсюда [math]KM\perp BC[/math]

[math]С_1С\perp(ABC)[/math], как высота прямой призмы, тогда [math]С_1С\perp KM[/math], поскольку [math]KM[/math] лежит в плоскости [math](ABC)[/math], [math]KM\perp(BB_1C_1)[/math] по признаку перпендикулярности прямой и плоскости. Следовательно по признаку перпендикулярности плоскостей следует, что [math](C_1MK)\perp(BB_1C_1)[/math], так как [math](C_1MK)[/math] содержит прямую [math]KM[/math]. Значит [math](KC_1M)[/math] - искомое сечение.

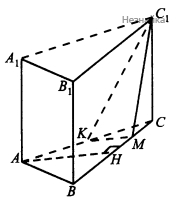
б) Проекция [math]C_1K[/math] на плоскость [math]BB_1C_1C[/math]: [math]MK\perp BC,\;C_1M[/math] - проекция [math]C_1K[/math]. [math]\angle KC_1M[/math] - искомый угол.

[math]\cos\angle KC_1M=\frac{C_1M^2+C_1K^2-MK^2}{2C_1M\times C_1K}[/math]

[math]\begin{array}{l}С_1M=\sqrt{C_1C^2+MC^2}=\sqrt{6+1}=\sqrt7\\C_1K=\sqrt{CC_1^2+CK^2}=\sqrt{6+4}=\sqrt{10}\\MK=KC\times\sin60^\circ=2\times\frac{\sqrt3}2=\sqrt3\end{array}[/math]

[math]\cos\angle KC_1M=\frac{7+10-3}{2\times\sqrt{70}}=\frac{14}{2\sqrt{70}}=\frac{\sqrt{70}}{10}[/math]

Ответ: [math]\frac{\sqrt{70}}{10}[/math]