Решение:

Приведем данное уравнение к виду:

[math]x^{10}+x^2=(2a+2\left|x\right|+a^2)^5+2a+2\left|x\right|+a^2[/math] или [math]f(x^2)=f(2a+2\left|x\right|+a^2)[/math], где [math]f(p)=p^5+p[/math]. Так как производная [math]f`(p)=5p^4+1>0[/math] всегда больше нуля, то функция возрастает на всей области определения. Следовательно получаем равносильно уравнение [math]x^2=2a+2\left|x\right|+a^2[/math] или [math]x^2-2\left|x\right|-2a-a^2=0[/math]

Пусть [math]\left|x\right|=t[/math], тогда получим квадратное уравнение [math]t^2-2t-2a-a^2=0[/math], имеющее корни [math]t=-a;\;t=a+2[/math]. отсюда запишем [math]\left|x\right|=-a;\;\left|x\right|=a+2[/math] . Построим графики функций [math]a(x)=-\left|x\right|;\;a(x)=\left|x\right|-2[/math] . Первый график имеет "вершину" (0;0), а второй - (0;2). Решая систему [math]\left\{\begin{array}{l}a=-\left|x\right|\\a=\left|x\right|-2\end{array}\right.[/math] найдем координаты двух общих точек (-1;1) и (1;-1)

Рассмотрим семейство горизонтальных прямых.

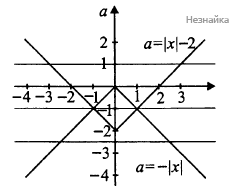
При [math]a\in(-\infty;-2)\cup\{-1\}\cup(0;+\infty)[/math] эти прямые пересекают построенный график, состоящий из двух уголков, ровно в двух точках. Значит, данное уравнение имеет ровно два различных решения при [math]a\in(-\infty;-2)\cup\{-1\}\cup(0;+\infty)[/math]

Ответ: [math](-\infty;-2)\cup\{-1\}\cup(0;+\infty)[/math]