Вариант 4
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
Магазин покупает средство от комаров по 140 рублей за флакон и продаёт с наценкой 25%. Какое наибольшее число флаконов можно купить в этом магазине на 3000 рублей?
На диаграмме показано распределение продаж чайных кружек за месяц в 10 магазинах .Среди представленных магазинов первое место по продаже чайных кружек занимает магазин Е, а десятое — И. Какое место занимает магазин Д?

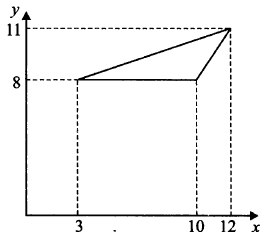
Найдите площадь треугольника, вершины которого имеют координаты (3; 8), (10; 8), (12; 11)
Из множества чисел от 20 до 29 наудачу выбирают одно число. Какова вероятность того, что оно делится на 4?
Решите уравнение 23+х = 0,4 • 53+х.
Основания равнобедренной трапеции равны 19 и 75. Тангенс острого угла равен 3/14. Найдите высоту трапеции.
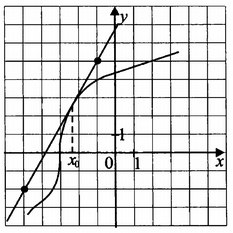
На рисунке изображён график функции у = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
Прямоугольный параллелепипед описан около сферы радиуса 20. Найдите его объём.
Найдите значение выражения [math]\frac{24\sin298^\circ}{\sin62^\circ}[/math]
В розетку электросети подключены приборы, общее сопротивление которых составляет R1 = 48 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R2 этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R1 Ом и R2 Ом их общее сопротивление задаётся формулой [math]R=\frac{R_1R_2}{R_1+R_2}[/math](Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 16 Ом. Ответ выразите в омах.
Компания «Эгеушер» начала инвестировать средства в перспективную отрасль в 2008 году, имея капитал в размере 8000 долларов. Каждый год, начиная с 2009 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Незнайка» начала инвестировать средства в другую отрасль в 2010 году, имея капитал в размере 10 000 долларов, и начиная с 2011 года ежегодно получала прибыль, составляющую 300% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2013 года, если прибыль из оборота не изымалась?
Найдите наименьшее значение функции [math]y=\frac34x^\frac43-2x+2[/math]
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math]3\times4^x-7\times10^x+2\times25^x=0[/math]
б) Укажите корни этого уравнения, принадлежащие отрезку [0; 3].
Решение:
а) [math]3\times2^{2x}-7\times2^x\times5^x+2\times5^{2x}=0[/math]
[math]3\times\frac{2^{2x}}{5^{2x}}-7\times\frac{2^x}{5^x}+2=0,\;\left(\frac25\right)^x=t,\;t>0[/math]
[math]3t^2-7t+2=0,\;t_1=2,\;t_2=\frac13[/math]
[math]\left(\frac25\right)^x=\frac13,\;x=\log_\frac25\frac13;\;\;\;\;\;\left(\frac25\right)^x=2,\;x=\log_\frac252[/math]
б) [math]\;\log_\frac252<0[/math]
[math]\log_\frac25\frac13\;\;\;\in\left[0;3\right][/math]
Ответ: а) [math]\log_\frac25\frac13\;[/math], [math]\log_\frac252[/math]; б) [math]\log_\frac25\frac13[/math]
В правильной треугольной призме ABCA1B1C1 точка О — центр основания треугольника АВС, точки O1 и О2 — центры симметрий боковых граней АА1В1В и АА1С1С соответственно.
а) Постройте сечение призмы плоскостью OO1O2.
б) Найдите угол между плоскостью АВС и плоскостью OO1O2, если сторона основания призмы равна 9, а площадь сечения призмы плоскостью OO1O2 равна [math]13,5\sqrt3[/math].
a) Сечение, проходящее через точку[math]O[/math], - центр [math]\bigtriangleup ABC[/math], точки [math]O_1[/math] и [math]O_2[/math] - центры симметрии боковых граней [math]AA_1B_1B[/math] и [math]AA_1C_1C[/math].
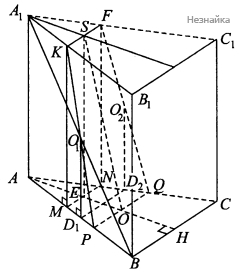
Пусть [math]D_1D_2[/math] проекция отрезка [math]O_1O_2[/math] на плоскость [math]ABC[/math]. По условию призма правильная, значит, [math]AA_1B_1B[/math] и [math]AA_1C_1C[/math] равные прямоугольники, поэтому расстояния от точек [math]O_1[/math] и [math]O_2[/math] до сторон [math]AB[/math] и [math]AC[/math] равны, то есть [math]O_1D_1=O_2D_2[/math]. Получаем прямоугольник [math]D_1O_1O_2D_2[/math], у которого [math]O_1O_2\;\parallel D_1D_2[/math], следовательно, по признаку параллельности прямой и плоскости прямая [math]O_1O_2[/math] параллельна плоскости [math]ABC[/math]
Сечение[math]OO_1O_2[/math] проходит через прямую [math]O_1O_2[/math], значит, пересекает плоскость [math]ABC[/math] по прямой, параллельной [math]O_1O_2[/math]. Проведем через точку [math]O[/math] прямую [math]PQ[/math], параллельную [math]D_1D_2[/math]. Прямые [math]PO_1[/math] и [math]QO_2[/math] пересекают плоскость [math]A_1B_1C_1[/math] в точках [math]K[/math] и [math]F[/math] соответственно. Четырехугольник [math]PKFQ[/math] - искомое сечение
б) По свойству параллельных плоскостей [math]PQ\parallel KF[/math], следовательно, четырехугольник [math]PKFQ[/math] - трапеция
Так как [math]O_1D_1\parallel AA_1\parallel BB_1[/math] и расстояния от точки [math]O_1[/math] до ребер [math]AA_1[/math] [math]BB_1[/math] равны, то равны расстояния [math]AD_1[/math] и [math]BD_1[/math], аналогично равны [math]AD_2[/math] и [math]CD_2[/math], значит, [math]D_1D_2[/math] - средняя линия треугольника [math]ABC[/math]. [math]D_1D_2\parallel O_1O_2\parallel PQ\parallel BC[/math]
Проведем [math]KM\perp AB[/math] и [math]FN\perp AC[/math], тогда трапеция [math]MPQN[/math] - проекция трапеции [math]KPQF[/math] на плоскость [math]ABC[/math]
Пусть [math]AH[/math] - высота [math]\bigtriangleup ABC[/math], [math]SO[/math] - высота трапеции [math]KPQF[/math], значит [math]\angle SOA[/math] - линейный угол двугранного угла между плоскостью сечения и плоскостью основания
[math]\cos\angle SOA=\frac{S_{MPQN}}{S_{KPQF}}[/math]
Из равенства треугольников [math]A_1O_1K[/math] и [math]BO_1P[/math] по II признаку следует, что [math]A_1K=BP,\;A_1K=AM[/math] как противоположные стороны прямоугольника[math]AA_1KM[/math]. Имеем [math]AM=PB[/math]. Так как [math]PQ\parallel BC[/math] и проходит через центр равностороннего треугольника, то [math]AM=MP=PB=3[/math]. Проведем [math]SE\perp MN[/math]
Высота [math]AH[/math] точками [math]E[/math] и [math]O[/math] делится на три равные части. [math]EO=\frac13AH=\frac13\frac{9\sqrt3}2=\frac{3\sqrt3}2[/math], а проекции [math]PQ[/math] и [math]MN[/math] соответственно равны [math]PQ=\frac23BC=\frac23\times9=6,\;MN=\frac13BC=3.[/math]
[math]S_{MPQN}=\frac{MN+PQ}2\times EO=\frac{3+6}2\times\frac{3\sqrt3}2=\frac{27\sqrt3}4[/math]
[math]\begin{array}{l}\cos\angle SOA=\frac{27\sqrt3}{4\times13,5\sqrt3}=\frac12\\\angle SOA=60^\circ\end{array}[/math]
Ответ: [math]60^\circ[/math]
Решите систему неравенств [math]\left\{\begin{array}{l}2^x+\frac{22}{2^x}\geq13,\\x\log_{x+2}(5-2x)\leq0\end{array}\right.[/math]
Решение:
1) [math]2^x+\frac{22}{2^x}\geq13[/math]
Пусть[math]2^x=t,\;t>0[/math]
[math]\left\{\begin{array}{l}t+\frac{22}t-13\geq0\\t>0\end{array}\right.\left\{\begin{array}{l}t^2-13t+22\geq0\\t>0\end{array}\right.\left\{\begin{array}{l}(t-11)(t-2)\geq0\\t>0\end{array}\right.[/math]
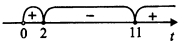
[math]\begin{array}{l}0<t\leq2,\;t\geq11\\0<2^x\leq2,\;2^x\geq11\\x\leq1,\;x\geq\log_211\end{array}[/math]
2) [math]\begin{array}{l}x\log_{x+2}(5-2x)\leq0\\x(\log_{x+2}(5-2x)-\log_{x+2}1)\leq0\end{array}[/math]
ОДЗ: [math]\left\{\begin{array}{l}\begin{array}{c}x+2>0\\x+2\neq1\end{array}\\5-2x>0\end{array}\right.[/math]
[math]x\in(-2;-1)\cup(-1;2,5)[/math]
На ОДЗ выражение [math]\log_{x+2}(5-2x)-\log_{x+2}1[/math] совпадает по знаку с выражением [math](x+2-1)(5-2x-1).[/math]
Получим [math]x(x+1)(4-2x)\leq0[/math], [math]x(x+1)(x-2)\geq0[/math], [math]x\in\lbrack-1;0\rbrack\cup\lbrack2;+\infty)[/math]
Учитывая ОДЗ, получим [math]x\in(-1;0\rbrack\cup\lbrack2;2,5)[/math]
Объединим полученные решения в систему.
[math]\left\{\begin{array}{l}x\in(-1;0\rbrack\cup\lbrack2;2,5);\\x\leq1,\;x\geq\log_211.\end{array}\right.[/math]
Так как [math]\log_211>\log_28=3[/math], то решением системы является промежуток [math](-1;0\rbrack[/math]
Ответ: [math](-1;0\rbrack[/math]
Внутри прямого угла АОВ проведён луч ОС. В угол ВОС вписана окружность, касающаяся лучей ОВ и ОС в точках B и C соответственно, в угол АОС вписана окружность, касающаяся лучей ОА и ОС в точках А и С соответственно. Радиус одной из этих окружностей в 4 раза больше радиуса другой.
а) Докажите, что ОА = ОВ.
б) Найдите косинус меньшего из углов АОС и ВОС.
Решение:
а) Не нарушая общности, можем считать, что большая окружность вписана в угол [math]AOC[/math]. Пусть [math]CQ=r;\;PC=4r[/math]. так как окружность с центром [math]P[/math] вписана в угол [math]AOC[/math], то [math]PA\perp OA,\;PC\perp OC,\;OA=OC[/math] как отрезки касательных, проведенные из одной точки. аналогично [math]OC=OB[/math], тогда [math]OA=OB[/math], что и требовалось доказать.
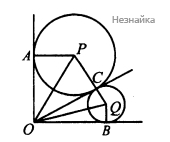
б) Из того, что [math]PO[/math] и [math]QO[/math] - биссектрисы углов [math]AOC[/math] и [math]BOC[/math] соответственно, следует, что [math]\angle POQ=45^\circ[/math]
Обозначим [math]OA=OB=OC=x[/math], тогда [math]OP=\sqrt{16r^2+x^2\;},\;OQ=\sqrt{r^2+x^2},\;PQ=4r+r=5r[/math]. Учитывая, что [math]\angle POQ=45^\circ,[/math] по теореме косинусов имеем [math]PQ^2=OP^2+OQ^2-2OP\times OQ\times\frac{\sqrt2}2[/math]
[math]16r^2+x^2+r^2+x^2-\sqrt2\sqrt{16r^2+x^2}\sqrt{r^2+x^2}=25r^2[/math], решая уравнение относительно [math]x^2[/math] , получим [math]x^2=\frac{33\pm5\sqrt{41}}2r^2[/math]
[math]\cos\angle COQ=\frac{OC}{OQ}=\frac x{\sqrt{r^2+x^2}}=\sqrt{\frac{33\pm5\sqrt{41}}{35\pm5\sqrt{41}}}.[/math]
Если [math]\cos\angle COQ=\sqrt{\frac{33-5\sqrt{41}}{35-5\sqrt{41}}}.[/math], то [math]\cos\angle BOC=\cos(2\angle COQ)=2\cos^2\angle COQ-1=2\times\frac{33-5\sqrt{41}}{35-5\sqrt{41}}-1=\frac{31-5\sqrt{41}}{35-5\sqrt{41}}<0[/math], что противоречит тому, что [math]\angle BOC<90^\circ[/math]
Если [math]\cos\angle COQ=\sqrt{\frac{33+5\sqrt{41}}{35+5\sqrt{41}}},[/math] то [math]\cos\angle BOC=\cos(2\angle COQ)=2\cos^2\angle COQ-1=2\times\frac{33+5\sqrt{41}}{35+5\sqrt{41}}-1=\frac{3+\sqrt{41}}{10}[/math]
Ответ: [math]\frac{3+\sqrt{41}}{10}[/math].
Производительность первого цеха завода не более 730 произведённых телевизоров в сутки.
Производительность второго цеха завода до реконструкции составляла 75% от производительности первого цеха. После реконструкции второй цех увеличил производительность на 20% и стал выпускать более 640 телевизоров в сутки.
Найдите, сколько телевизоров в сутки выпускает второй цех после реконструкции, если оба цеха выпускают в сутки целое число телевизоров
Решение:
Пусть первый цех в сутки выпускает [math]x[/math] телевизоров, тогда до реконструкции второй цех выпускал [math]0,75x[/math] телевизоров, при этом [math]0,75x\in\mathbb{N}[/math] и [math]x\in\mathbb{N}[/math], значит [math]x[/math] - кратно 4.
После реконструкции второй цех стал выпускать [math]0,75x\times1,2=0,9x[/math] телевизоров, при этом [math]0,9x\in\mathbb{N}[/math], значит [math]x[/math] кратно 10.
Таким образом [math]x[/math] кратно 20.
По условию [math]x\leq730[/math] и [math]0,9x>640[/math] или [math]x>711[/math]
Число, кратное 20 и [math]711<x\leq730[/math], это число [math]720[/math]. Второй цех после реконструкции стал выпускать [math]720\times0,9=648[/math] телевизоров в сутки.
Ответ: 648
Найдите все значения а, для каждого из которых уравнение [math]х^{10}-(2a\;+\;2\vert х\vert\;+\;а^2)^5\;+\;х^2\;=\;2а\;+\;2\vert х\vert\;+\;а^2[/math] имеет ровно два различных решения.
Решение:
Приведем данное уравнение к виду:
[math]x^{10}+x^2=(2a+2\left|x\right|+a^2)^5+2a+2\left|x\right|+a^2[/math] или [math]f(x^2)=f(2a+2\left|x\right|+a^2)[/math], где [math]f(p)=p^5+p[/math]. Так как производная [math]f`(p)=5p^4+1>0[/math] всегда больше нуля, то функция возрастает на всей области определения. Следовательно получаем равносильно уравнение [math]x^2=2a+2\left|x\right|+a^2[/math] или [math]x^2-2\left|x\right|-2a-a^2=0[/math]
Пусть [math]\left|x\right|=t[/math], тогда получим квадратное уравнение [math]t^2-2t-2a-a^2=0[/math], имеющее корни [math]t=-a;\;t=a+2[/math]. отсюда запишем [math]\left|x\right|=-a;\;\left|x\right|=a+2[/math] . Построим графики функций [math]a(x)=-\left|x\right|;\;a(x)=\left|x\right|-2[/math] . Первый график имеет "вершину" (0;0), а второй - (0;2). Решая систему [math]\left\{\begin{array}{l}a=-\left|x\right|\\a=\left|x\right|-2\end{array}\right.[/math] найдем координаты двух общих точек (-1;1) и (1;-1)
Рассмотрим семейство горизонтальных прямых.
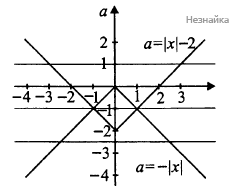
При [math]a\in(-\infty;-2)\cup\{-1\}\cup(0;+\infty)[/math] эти прямые пересекают построенный график, состоящий из двух уголков, ровно в двух точках. Значит, данное уравнение имеет ровно два различных решения при [math]a\in(-\infty;-2)\cup\{-1\}\cup(0;+\infty)[/math]
Ответ: [math](-\infty;-2)\cup\{-1\}\cup(0;+\infty)[/math]
На n деревьях, расположенных по окружности, сидели n весёлых чижей (на каждом дереве по чижу). Время от времени два чижа одновременно перелетают на соседние деревья в противоположных направлениях (один по часовой стрелке, другой — против). Могут ли все n чижей собраться на одном дереве, если
а) n = 5?
б) n = 2019?
в) n = 12?
Решение:
а) Занумеруем деревья числами 1,2,3,4,5 (по порядку). Пусть один чиж сидит неподвижно, например, на дереве 3, тогда чижи с деревьев 2 и 4, совершив по одному перелету, окажутся на дереве 3, а чижи с деревьев 1 и 5, совершив по два перелета, окажутся на дереве 3. Итак, все пять чижей могут собраться на одном дереве.
б) Пусть один чиж сидит неподвижно на дереве. Разобьем остальных чижей на пары сидящих на одинаковом расстоянии [math]r[/math] перелетов от неподвижного в ту и другую сторону ( [math]r=1,2,...,1009[/math]). Ясно, что каждая такая пара может за [math]r[/math] перелетов попасть на то дерево, где сидит неподвижный чиж.
в) Занумеруем деревья по порядку, например, по часовой стрелке числами от 1 до 12. Пусть количество чижей на [math]k[/math]-м дереве в какой то момент времени равно [math]a_k[/math]. Рассмотрим выражение [math]S=1\times a_1+2\times a_2+...+12\times a_{12}[/math]
Покажем, что когда два чижа перелетают на соседние деревья, то [math]S[/math] либо не меняется, либо изменяется на 12. Действительно, пусть какой-то чиж перелетает с [math]k[/math]-го дерева на следующее по часовой стрелке. Тогда в сумме [math]S[/math] меняются 2 слагаемых. Если [math]k<12[/math], то меняются [math]k[/math]-е и [math]k+1[/math]-е слагаемые, и их сумма становится равной [math]k(a_k-1)+(k+1)(a_{k+1}+1)=ka_k+(k+1)a_{k+1}+1[/math], т.е. увеличивается на 1.
При перелете двух чижей на соседние деревья, очевидно, что сумма или не меняется или меняется на 12. В начальный момент времени на каждом дереве сидело по 1 чижу.
[math]S=1\times1+2\times1+...12\times1=78[/math]
Таким образом, после любого целого числа перелетов сумма будет равна [math]78+12p[/math], где [math]p[/math] - целое число. Если бы все чижи собрались на [math]q[/math]-м дереве, то [math]S=12q[/math], то есть выполнялось бы равенство [math]78+12p=12q[/math], а потому 78 должно делиться на 12, что неверно. Значит, требуемое невозможно.
Ответ: а)да; б) да; в) нет.
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||