Задание № 8193
В выпуклом пятиугольнике ABCDE диагонали BE и СЕ являются биссектрисами неравных углов при вершинах В и С соответственно.
а) Докажите, что точка Е есть центр вписанной или вневписанной окружности треугольника ОСВ, где О — точка пересечения прямых CD и АВ.
б) Найдите площадь пятиугольника ABCDE, если ∠А = 37°, ∠D = 143°, а площадь треугольника ВСЕ равна 13.
Решение:
а) Пусть точки [math]O[/math] и [math]E[/math] расположены по одну сторону от прямой [math]BC[/math] (см. рисунок), то есть [math]\angle B+\angle C=180^\circ[/math], тогда [math]BE[/math] и [math]CE[/math] являются биссектрисами внутренних углов при вершинах [math]B[/math] и [math]C[/math] соответственно треугольника [math]BCO[/math]. По свойству биссектрисы [math]BE[/math] точка [math]E[/math] равноудалена от сторон [math]BO[/math] и [math]BC[/math]. Аналогично по свойству биссектрисы [math]CE[/math] точка [math]E[/math] равноудалена от сторон [math]BC[/math] и [math]OC[/math]. Следовательно, точка [math]E[/math] равноудалена от всех сторон треугольника [math]BCO[/math] и является центром окружности, вписанной в этот треугольник.
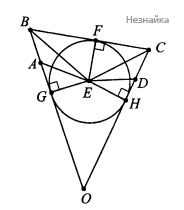
Рассмотрим другой случай. Пусть точки [math]O[/math] и [math]E[/math] расположены по разные стороны от прямой [math]BC[/math](см. рисунок ниже), то есть [math]\angle B+\angle C>180^\circ[/math], тогда [math]BE[/math] и [math]CE[/math] являются биссектрисами внешних углов при вершинах [math]B[/math] и [math]C[/math] cсоответственно треугольника [math]BCO[/math]. По свойству биссектрисы [math]BE[/math] точка [math]E[/math] равноудалена от прямых [math]BO[/math] и [math]BC[/math]. Аналогично точка [math]E[/math] равноудалена от прямых [math]BC[/math] и [math]OC[/math]. Следовательно, точка [math]E[/math] равноудалена от стороны [math]BC[/math] и продолжений сторон [math]BO[/math] и [math]OC[/math] треугольника [math]BCO[/math] и является центром вневписанной окружности этого треугольника. [math]EG,EF,EH\;-\;[/math] радиусы этой окружности.
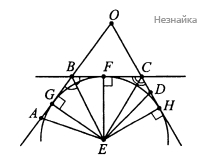
б) Сумма углов выпуклого пятиугольника равна [math]540^\circ[/math]. По условию задачи [math]\angle A=37^\circ,[/math][math]\angle D=143^\circ,[/math][math]\angle A+\angle D=180^\circ[/math]. Если [math]\angle B+\angle C=180^\circ,[/math], что противоречит условию выпуклости прямоугольника. Значит [math]\angle B+\angle C>180^\circ,[/math], поэтому: [math]\bigtriangleup AGE=\bigtriangleup DHE[/math] по катету и острому углу. Аналогично [math]\bigtriangleup EHC=\bigtriangleup EFC.\;[/math] Последовательно имеем:
[math]S_{ABE}+S_{CDE}=S_{AGE}+S_{GBE}+S_{CHE}-S_{DHE}=S_{GBE\;}+\;S_{CHE}=[/math][math]=S_{BFE}+S_{FCE}=S_{BCE}=13[/math]
[math]S_{ABCDE}=S_{ABE}+S_{CDE}+S_{BCE}=13+13=26[/math]
Ответ: 26
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.