Решение:

а) Заметим, что [math]OA\perp AC[/math] и [math]O_1C\perp AC[/math] по свойству радиусов, проведенных в точку касания (см. рисунок). Опустим [math]OK\perp OC_{1\;}[/math] ([math]K[/math] лежит на [math]O_1C[/math]). Пусть [math]OA[/math] равно [math]R[/math], тогда [math]O_1C=3R,\;OACK[/math] - прямоугольник, [math]KC=OA=R[/math]. Значит, [math]O_1K=2R[/math]. [math]M[/math] - точка касания окружностей, [math]OM=R,\;O_1M=3R[/math]. В прямоугольном треугольнике [math]OO_1K[/math] катет [math]O_1K=2R[/math], гипотенуза [math]OO_1=OM+MO_1=4R,[/math] то есть катет [math]O_1K[/math] равен половине гипотенузы, откуда [math]\angle O_1OK=30^\circ[/math], [math]\angle AOO_1=\angle AOK+\angle O_1OK=120^\circ[/math], что и требовалось доказать.

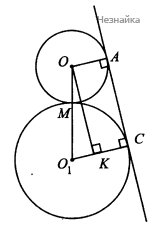
В треугольнике [math]OO_1K[/math] по теореме Пифагора [math]OK=\sqrt{(4R)^2-(2R)^2}=2\sqrt3R.[/math] [math]AC=OK=2\sqrt3R=6\sqrt3,\;[/math] следовательно, [math]R=3.[/math]. Длина окружности с центром [math]O[/math] равна [math]2\mathrm{πR}=6\mathrm\pi[/math]. Длина окружности с центром [math]{\mathrm O}_1[/math] равна [math]2\mathrm\pi(3\mathrm R)=18\mathrm\pi[/math]. [math]\angle A_1OA=360^\circ-\angle AOO_1-\angle A_1OO_1=120^\circ[/math] (см. рисунок). Значит длина внешней дуги меньшей окружности равна[math]6\mathrm\pi\frac{120^\circ}{360^\circ}=2\mathrm\pi[/math]. Ясно, что [math]\angle{\mathrm{OO}}_1\mathrm C=60^\circ,[/math][math]\angle{\mathrm{CO}}_1{\mathrm C}_1=120^\circ,[/math], значит длина внешней дуги большей окружности равна [math]\frac{240^\circ}{360^\circ}\times18\mathrm\pi=12\mathrm\pi[/math]

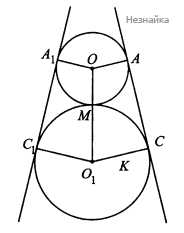
искомый периметр равен [math]{\mathrm A}_1{\mathrm C}_1+2\mathrm\pi+\mathrm{AC}+12\mathrm\pi=12\sqrt3+14\mathrm\pi[/math]

Ответ: [math]12\sqrt3+14\mathrm\pi[/math]