Демонстрационный вариант

Математика Профильный уровень

Часть 1

Ответом на задания 1—12 должно быть целое число или десятичная дробь.

Поезд отправился из Санкт-Петербурга в 23 часа 50 минут и прибыл в Москву в 7 часов 50 минут следующих суток. Сколько часов поезд находился в пути?

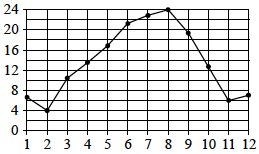
На рисунке точками показана средняя температура воздуха в Сочи за каждый месяц 1920 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Для наглядности точки соединены линией. Определите по рисунку, сколько месяцев из данного периода средняя температура была больше 18 градусов Цельсия.

Демонстрационный вариант

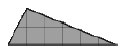
На клетчатой бумаге с размером клетки 1 см × 1 см изображён треугольник. Найдите его площадь. Ответ дайте в см².

Демонстрационный вариант

В сборнике билетов по биологии всего 25 билетов. Только в двух билетах встречается вопрос о грибах. На экзамене школьнику достаётся один случайно выбранный билет из этого сборника. Найдите вероятность того, что в этом билете будет вопрос о грибах.

Найдите корень уравнения $3^{x-5}=81$ .

Треугольник ABC вписан в окружность с центром O. Найдите угол BOC, если угол BAC равен 32. Ответ дайте в градусах.

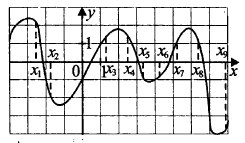
На рисунке 47 изображен график y = f'(x) — производной функции f(x). На оси абсцисс отмечено девять точек: x₁, x₂, ... x₉. Сколько из этих точек лежат на промежутках возрастания функции f(x)?

Демонстрационный вариант

В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ выразите в см.

Найдите sin2α, если cosα = 0,6 и π < α < 2π.

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением $v=c\cdot\frac{f-f_0}{f+f_0}$ , где c = 1500 м/с — скорость звука в воде; f₀— частота испускаемого сигнала (в МГц); f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.

Весной катер идёт против течения реки в $1\frac23$ раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в $1\frac12$ раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Найдите точку максимума функции $y=\ln\left(x+4\right)^2+2x+7$ .

Часть 2.

При выполнении заданий 13—19 требуется записать полное решение и ответ.

а) Решите уравнение $\cos2x=1-\cos\left(\frac\pi2-x\right)$ .

б) Найдите все корни этого уравнения, принадлежащие промежутку [-5π/2; -π).

Показать ответ

а) Преобразуем обе части уравнения:

$1-2\sin^2x=1-\sin x;\;2\sin^2x-\sin x=0;\;\sin x(2\sin x-1)=0,$ откуда $\sin x=0$ или $\sin x=\frac12$

Из уравнения $\sin x=0$ находим: $x=\mathrm{πn},$ где $\mathrm n\in\mathbb{Z}$

Из уравнения $\sin x=\frac12$ находим: $x=(-1)^k\frac{\mathrm\pi}6+\mathrm{πk},$ где $\mathrm k\in\mathbb{Z}$

б) С помощью числовой окружности отберём корни уравнения, принадлежащие промежутку $\lbrack-\frac{5\mathrm\pi}2;-\mathrm\pi).$

Демонстрационный вариант

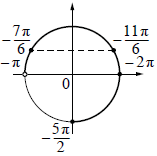
Получаем числа:

$-2\pi;\;-\frac{11\pi}6;\;-\frac{7\pi}6$ .

Ответ:

а) $\pi n,\;n\in\mathbb{Z};\;\left(-1\right)^k\frac\pi6+\pi k,\;k\in\mathbb{Z}$

б) $-2\pi;\;-\frac{11\pi}6;\;-\frac{7\pi}6$ .

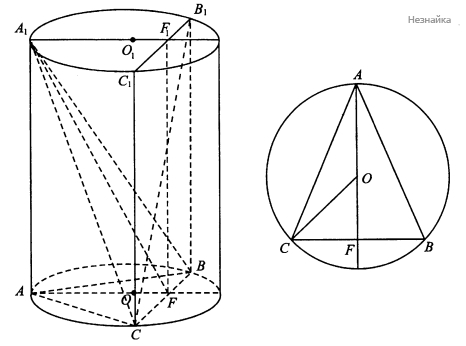
В основание цилиндра высотой 60 и радиусом основания 15 вписан остроугольный треугольник АВС, в котором ВС = 10, АВ = АС.

а) Постройте сечение призмы АВСА₁В₁С плоскостью, проходящей через точку А и перпендикулярную плоскостям СВВ₁и ВА₁С, если АА₁, ВВ₁и СС₁ — образующие цилиндра.

б) Найдите величину угла между плоскостями СВВ₁ и ВА₁С.

Показать ответ

Решение:

а) Пусть $O$ и $O_1$ - центры оснований цилиндра, тогда $F$ и $F_1$ - середины хорд $BC$ и $B_1C_1$ соответственно (см. рисунок) . Покажем, что $AFF_1$ - искомая плоскость. $A_1F$ - медиана, значит, и высота равнобедренного треугольника $A_1BC$ . $FF_1\parallel BB_1$ , значит, $FF_1\perp(ABC)$ и, в частности, $FF_1\perp BC$ . Так как $FF_1\perp BC$ и $A_1F\perp BC,\;$ $(AFF_1)\perp BC,\;$ , откуда $(AFF_1)\perp A_1BC\;$ и $(AFF_1)\perp BB_1C_1C\;$ . Сечением призмы $ABCA_1B_1C_1$ плоскостью $AFF_1$ является прямоугольник $AFF_1A_1$

б) Угол между плоскостями $CA_1B$ и $CBB_1$ - это угол $\angle A_1FF_1$

$\bigtriangleup A_1FF_1$ - прямоугольный, $tg\angle A_1FF_1=\frac{A_1F_1}{FF_1}$

$\bigtriangleup ABC$ - равнобедренный (по условию), $CF=\frac{BC}2=5$

$\bigtriangleup COF$ - прямоугольный, $OF=\sqrt{CO^2-CF^2}=\sqrt{15^2-5^2}=10\sqrt2$

$AF=AO+OF=15+10\sqrt2=5(3+2\sqrt2)$ $AF=A_1F_1$

$tg\angle A_1FF_1=\frac{5(3+2\sqrt2)}{60}=\frac{3+2\sqrt2}{12}$

Ответ: $arctg\;\frac{3+2\sqrt2}{12}$

Решите неравенство $\left(4-x\right)\left(2\log_{11}^2x-3\log_{11}x+1\right)>0$ .

Показать ответ

Решение:

ОДЗ: $x>0$

$\begin{array}{l}(4-x)(2\log_{11}^2x-3\log_{11}x+1)>0\\(x-4)(\log_{11}x-1)(2\log_{11}-1)<0\end{array}$

на ОДЗ выражение $\log_{11}x-1=\log_{11}x-\log_{11}11$ совпадает по знаку с выражением $x-11$ , выражение $2\log_{11}x-1=2(\log_{11}x-\log_{11}\sqrt{11})$ - с выражением $x-\sqrt{11}$ . Получим, что исходное неравенство на ОДЗ равносильно $(x-4)(x-\sqrt{11})(x-11)<0$ . Решив его методом интервалов, получим $x\in(-\infty;\;\sqrt{11})\cup(4;11)$ . Учитывая ОДЗ, $x\in(0;\;\sqrt{11})\cup(4;11)$

Ответ: $\left(0;\;\sqrt{11}\right)\cup\left(4;\;11\right)$ .

Две окружности с центрами О и О₁, радиусы которых относятся как 1 : 3, касаются внешним образом, длина их общей внешней касательной АС равна 6√3

а) Докажите, что угол АОО₁ равен 120° (ОА — радиус, проведённый в точку касания).

б) Найдите периметр фигуры, образованной внешними касательными и внешними дугами окружностей.

Показать ответ

Решение:

а) Заметим, что $OA\perp AC$ и $O_1C\perp AC$ по свойству радиусов, проведенных в точку касания (см. рисунок). Опустим $OK\perp OC_{1\;}$ ( $K$ лежит на $O_1C$ ). Пусть $OA$ равно $R$ , тогда $O_1C=3R,\;OACK$ - прямоугольник, $KC=OA=R$ . Значит, $O_1K=2R$ . $M$ - точка касания окружностей, $OM=R,\;O_1M=3R$ . В прямоугольном треугольнике $OO_1K$ катет $O_1K=2R$ , гипотенуза $OO_1=OM+MO_1=4R,$ то есть катет $O_1K$ равен половине гипотенузы, откуда $\angle O_1OK=30^\circ$ , $\angle AOO_1=\angle AOK+\angle O_1OK=120^\circ$ , что и требовалось доказать.

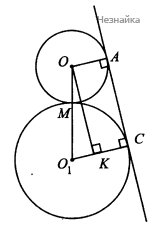
В треугольнике $OO_1K$ по теореме Пифагора $OK=\sqrt{(4R)^2-(2R)^2}=2\sqrt3R.$ $AC=OK=2\sqrt3R=6\sqrt3,\;$ следовательно, $R=3.$ . Длина окружности с центром $O$ равна $2\mathrm{πR}=6\mathrm\pi$ . Длина окружности с центром ${\mathrm O}_1$ равна $2\mathrm\pi(3\mathrm R)=18\mathrm\pi$ . $\angle A_1OA=360^\circ-\angle AOO_1-\angle A_1OO_1=120^\circ$ (см. рисунок). Значит длина внешней дуги меньшей окружности равна $6\mathrm\pi\frac{120^\circ}{360^\circ}=2\mathrm\pi$ . Ясно, что $\angle{\mathrm{OO}}_1\mathrm C=60^\circ,$ $\angle{\mathrm{CO}}_1{\mathrm C}_1=120^\circ,$ , значит длина внешней дуги большей окружности равна $\frac{240^\circ}{360^\circ}\times18\mathrm\pi=12\mathrm\pi$

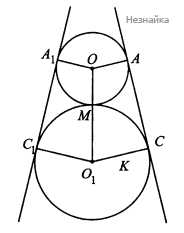
искомый периметр равен ${\mathrm A}_1{\mathrm C}_1+2\mathrm\pi+\mathrm{AC}+12\mathrm\pi=12\sqrt3+14\mathrm\pi$

Ответ: $12\sqrt3+14\mathrm\pi$

Предприниматель взял в аренду на 3 года помещения на условиях ежегодной платы (в конце года) С рублей. Имея некоторый первоначальный капитал, он удвоил его в течение года и оплатил аренду. Такая схема деятельности осуществлялась все три года. В результате в конце третьего года деятельности, после оплаты аренды предприниматель имел капитал в три раза превышающий первоначальный. Определите величину первоначального капитала, если аренда С составляла 12000 рублей.

Показать ответ

Пусть $x$ рублей первоначальный капитал предпринимателя, тогда $2x-С$ рублей - капитал после первого года

$2(2x-С)-C=4x-3c$ рублей - капитал после второго года.

$2(4x-3С)-C=8x-7c$ рублей - капитал после третьего года.

По условию к концу третьего года после оплаты аренды капитал предпринимателя в три раза превысил первоначальный, следовательно $8x-7c=3x$

$x=1,4\times12000=16800$

Ответ: 16800 рублей

Найдите все значения а, при которых любое решение уравнения $2\sqrt{9-4x}-7\log_\frac12(2-\frac12x)-4a=0$ принадлежит отрезку [-4; 0].

Показать ответ

Рассмотрим функцию $f(x)=2\sqrt{9-4x}-7\log_\frac12(2-\frac12x)$ . Она определена при $x\leq\frac94$ и убывает на всей области определения. Значит, уравнение $f(x)-4a=0$ может иметь только единственное решение (при соответствующих значениях параметра $a$ ). Это решение принадлежит отрезку $\lbrack-4;0\rbrack$ тогда и только тогда, когда $f(-4)-4a\geq0;\;f(0)-4a\leq0$ . Получаем систему неравенств:

$\left\{\begin{array}{l}10+14-4a\geq0\\6+7-4a\leq0\end{array}\right.\left\{\begin{array}{l}4a-24\leq0\\4a-13\geq0\end{array}\right.$

Откуда $\frac{13}4\leq a\leq6$

Ответ: $\left[\frac{13}4;6\right]$

Натуральное число называется палиндромом, если при расстановке его цифр в обратном порядке оно не изменяется (например, 8, 22, 171 и т.п.).

а) Сколько существует шестизначных палиндромов, каждая цифра в которых встречается не больше двух раз?

б) Существует ли пара натуральных чисел (а;b), таких, что никакая натуральная степень числа а не является палиндромом, а любая степень числа b является?

в) Сколько существует упорядоченных пар (х; у), где х,у — двузначные палиндромы, х≠y, x + у — палиндром, причём нечётный?

Показать ответ

Решение:

a) Шестизначный палиндром имеет вид $\overline{xyzzyx}$ . Цифру $x$ можно выбрать 9 способами (x $(x\neq0)$ ), после этого $y$ - тоже 9 способами $(y\neq x)$ , затем $z$ - 8 способами. Всего $9\times9\times8=648$ таких палиндромов.

б) Да, приведем примеры: $a=10,\;b=1.$ $a^n=10^n$ - не является палиндромом, $b^n=1$ - палиндром.

в) Все двузначные палиндромы, очевидно, имеют вид $11a$ , $1\leq a\leq9$ . Пусть первый палиндром равен $11\alpha$ , второй $11\beta$ , тогда их сумма - $11(\alpha+\beta)<200$ . Среди трехзначных чисел, меньших 200, все палиндромы имеют вид $1y1$ , где $y$ - цифра. На 11 из них делится только 121. Значит суммой двузначных палиндромов, являющейся палиндромом, может быть одно из чисел 33,55,.....,121, то есть одно из чисел $11t.\;3\leq t\leq11,\;t$ - нечетно. Для каждого $t$ найдем количество его представлений в виде суммы $\begin{array}{l}t=\alpha+\beta,\;(\alpha\neq\beta).\\\end{array}$

Если $\begin{array}{l}t=\alpha+\beta\\\end{array}$ , то $\begin{array}{l}\alpha=1,...,t-1\\\end{array}$ , при этом $\begin{array}{l}\alpha\neq\beta\\\end{array}$ , так как $t\;$ нечетно. То есть для каждого $t\;-(t-1)$ способов. Тогда искомое число вариантов равно $2+4+6+8+10=30$ .

Однако при таком подсчете для $t=11$ мы посчитали два лишних представления $(121=110+11=11+110)$ , так как число $110$ не является палиндромом. Значит, всего 30-2=28 вариантов.

Ответ: а) 648; б) да; в) 28.

0 из 0

№	Ваш ответ	Ответ и решение	Первичный балл
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения.