Задание № 8170
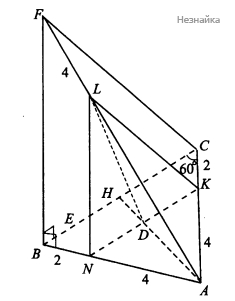
В треугольной пирамиде FABC основанием является правильный треугольник АВС, ребро FB перпендикулярно плоскости основания, стороны основания равны 6, а ребро FA равно 10. На ребре АС находится точка К, на ребре АВ — точка N, а на ребре AF — точка L. Известно, что FL = 4 и СК = BN = 2.
а) Постройте сечение пирамиды плоскостью, проходящей через точки К, N и L
б) Найдите площадь этого сечения
Решение:
Так как [math]FB\;\perp\;(ABC)[/math], то [math]FB\;\perp\;AB[/math] и [math]FB\;\perp\;BC[/math] (см. рисунок).
Из прямоугольных треугольников [math]FAB[/math] и [math]FBC[/math] получим [math]FB=\sqrt{AF^2-AB^2}=8,\;FC=\sqrt{FB^2+BC^2}=10[/math]
[math]\cos\angle FAB=\frac{AB}{AF}=0,6[/math], тогда из [math]\bigtriangleup ANL[/math] по теореме косинусов [math]NL^2=AN^2+AL^2-2AN\times NL\times\cos\angle FAB=\frac{29}5\times4[/math]
[math]NL=2\times\frac{\sqrt{29}}{\sqrt5}[/math]
Из [math]\bigtriangleup FAC[/math]: [math]\cos\angle FAC=\frac{AF^2+AC^2-FC^2}{2\times AF\times AC}=0,3[/math]
Из [math]\bigtriangleup ALK[/math] по теореме косинусов [math]LK^2=AL^2+AK^2-2AL\times AK\times\cos\angle FAC=\frac{47}5\times4[/math]
[math]LK=\frac{\sqrt{47}}{\sqrt5}\times2,\;NK=4.[/math]
[math]\cos\angle LNK=\frac{{\displaystyle\frac{4\times29}5}+16-{\displaystyle\frac{4\times47}5}}{2\times{\displaystyle\frac{2\sqrt{29}}{\sqrt5}}\times4}=\frac1{2\sqrt{145}}[/math]
[math]sin\angle LNK=\sqrt{1-\frac1{580}}=\frac{\sqrt{579}}{2\sqrt{145}}[/math]
[math]S_{KLN}=\frac12LN\times NK\times sin\angle LNK=0,4\sqrt{579}[/math]
Ответ: [math]0,4\sqrt{579}[/math]
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.