Решение:

1) [math]5^x+\frac{20}{5^x}-9\geq0.[/math]

[math]\frac{(5^x)^2-9\times5^x+20}{5^x}\geq0,\;5^x=t,\;t>0[/math]

[math]\frac{t^2-9t+20}t\geq0[/math]

[math]\frac{(t-4)(t-5)}t\geq0[/math]

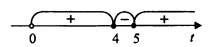
[math]0<t\leq4;\;t\geq5[/math]

[math]0<5^x\leq5^{\log_54};\;5^x\geq5^1[/math]

[math]x\leq\log_54;\;x\geq1[/math]

2) [math]\log_{x+5}(\frac{x+2}5)\leq\log_{x+5}1[/math]

ОДЗ: [math]\left\{\begin{array}{l}x+5>0\\x+5\neq1\\x+2>0\end{array}\right.[/math] [math]x>-2[/math]

На ОДЗ выражение [math]\log_{x+5}(\frac{x+2}5)-\log_{x+5}1[/math] совпадает по знаку с выражением (x+5-1)(x/5+0,4-1).

Получим [math](x+4)(x-3)\leq0[/math]

[math]-4\leq x\leq3[/math] с учетом ОДЗ получаем: [math]-2<x\leq3[/math]

3) Решим систему [math]\left\{\begin{array}{l}x\leq\log_54,\;x\geq1\\-2<x\leq3\end{array}\right.\;\;\left\{\begin{array}{l}-2<x\leq\log_54\\1\leq x\leq3\end{array}\right.[/math]

Ответ: [math]\;(-2;\log_54\rbrack,\lbrack1;3\rbrack.[/math]