Вариант 5
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
На бензоколонке один литр бензина стоит 31 рубль 50 копеек. Водитель залил в бак 40 л бензина и купил бутылку воды за 52 рубля. Сколько рублей сдачи он получит с 2000 рублей?
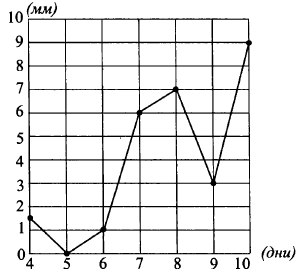
На рисунке изображён график осадков в городе N с 4 по 10 февраля 1994 года. На оси абсцисс откладываются дни, на оси ординат — количество осадков (в мм). Определите по рисунку, сколько дней из данного периода выпадало от 2 до 8 мм осадков.
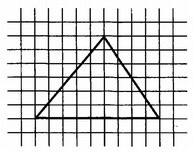
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см. Ответ дайте в квадратных сантиметрах.
На улице неправильно припарковано 48 автомобилей, среди которых автомобиль Маши. Эвакуатор выбрал случайным образом и вывез на штрафстоянку 12 автомобилей. Какова вероятность, что автомобиль Маши не вывезли на штрафстоянку?
Решите уравнение [math]x=\frac{12-6x}{x-5}[/math]
Если уравнение имеет более одного корня, в ответе укажите больший из них.
В треугольнике АВС угол С равен 90°, СН — высота, АВ = 144, [math]\sin A=\frac56[/math] . Найдите BH.
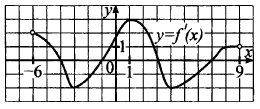
На рисунке изображён график у = f'(x) — производной функции f(x), определённой на интервале (—6; 9). Найдите промежутки возрастания f(x). В ответе укажете длину наибольшего из них.
Во сколько раз увеличится площадь поверхности октаэдра, если все рёбра увеличить в 1,5 раза?
Найдите значение выражения [math]\frac{104\sin17^\circ\times\cos17^\circ}{\sin34^\circ}[/math]
Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе показателей информативности In, оперативности Ор, объективности Тr публикаций, а также качества Q сайта. Каждый отдельный показатель — целое число от 1 до 7.
Составители рейтинга считают, что объективность ценится вчетверо, информативность публикаций втрое, а оперативность вдвое дороже, чем качество сайта. Таким образом, формула приняла вид:
[math]y=\frac{3In+2Op+4Tr+Q}A[/math]
Найдите, каким должно быть число А, чтобы издание, у которого все показатели максимальны, получило рейтинг 2.
Заказ на 450 деталей один рабочий выполняет на 15 часов быстрее второго. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 15 деталей больше?
Найдите наименьшее значение функции у = 4(х + 9)2 е 4х+1 на отрезке [-9,5; -0,25].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
а) Решите уравнение [math]\sqrt3\sin^22x-2\sin4x+\sqrt3\cos^22x=0[/math]
б) Укажите все корни этого уравнения, принадлежащие промежутку [math]\left[-1;1\right][/math]
Решение:
а) [math]\begin{array}{l}\sqrt3(\sin^22x+\cos^22x)-2\sin4x=0;\\\sqrt3-2\sin4x=0;\\\sin4x=\frac{\sqrt3}2.\end{array}[/math]
[math]\left\{\begin{array}{l}4x=\frac{\mathrm\pi}3+2\mathrm{πk},\;\mathrm k\in\mathbb{Z}\\4x=\frac{2\mathrm\pi}3+2\mathrm{πn},\;\mathrm n\in\mathbb{Z}\end{array}\right.\;\begin{array}{l}\left\{\begin{array}{l}x=\frac{\mathrm\pi}{12}+\frac\pi2k,\;\mathrm k\in\mathbb{Z}\\x=\frac{\mathrm\pi}6+\frac\pi2n,\;\mathrm n\in\mathbb{Z}\end{array}\right.\\\end{array}[/math]
б) Найдем корни этого уравнения, принадлежащие промежутку [math]\left[-1;1\right][/math]
При [math]k\geq1[/math] и [math]n\geq1[/math] корни принимают значения больше [math]1,5[/math] даже при грубом округлении [math]\mathrm\pi=3[/math]. Поэтому корни попадут в промежуток при значениях [math]\mathrm k=\mathrm n=0;[/math]
[math]x_1=\frac{\mathrm\pi}{12};\;x_2=\frac{\mathrm\pi}6[/math]
Ответ: а) [math]\frac{\mathrm\pi}6+\frac\pi2n;\;\frac{\mathrm\pi}{12}+\frac\pi2k;\;n,k\in\mathbb{Z}[/math]б) [math]x_1=\frac{\mathrm\pi}{12};\;x_2=\frac{\mathrm\pi}6[/math]
В прямой призме АВСА1В1С1 в основании лежит треугольник АВС со сторонами АВ = АС = 16, ВС = 10. Боковое ребро равно √33.
а) Постройте сечение призмы плоскостью, проходящей через прямую А1В и перпендикулярную плоскости СС1В1
б) Найдите косинус угла между А1В и плоскостью боковой грани СС1В1В.
В треугольнике [math]A_1B_1C_1[/math] проведем высоту [math]A_1H[/math]. Заметим, что [math]BB_1\perp(A_1B_1C_1)[/math], так как высота прямой призмы перпендикулярна плоскости основания. Тогда [math]BB_1\perp A_1H[/math], поскольку прямая [math]A_1H[/math] лежит в плоскости [math](A_1B_1C_1)[/math]. Тогда [math]A_1H\perp(CC_1B)[/math] по признаку перпендикулярности прямой и плоскости. Отсюда по признаку перпендикулярности плоскостей следует, что [math](BHA_1)\perp(CC_1B)[/math], так как плоскость [math](A_1B_1C_1)[/math] содержит прямую, перпендикулярную плоскости [math](CC_1B)[/math]. Значит [math]\bigtriangleup BHA_1[/math] - искомое сечение.
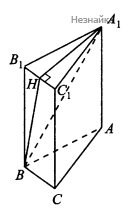
б) Так как [math]A_1H\perp(CC_1B_1)[/math], [math]BH[/math] является проекцией [math]BA_1[/math] на плоскость [math](CC_1B_1)[/math], а значит искомый угол равен углу [math]HBA_1[/math]. [math]A_1H[/math] - высота равнобедренного треугольника, проведенная к основанию, значит, [math]A_1H[/math] - медиана, [math]B_1H=\frac12B_1C_1=\frac12BC=5[/math]. [math]BH=\sqrt{BB_1^2+B_1H^2}=\sqrt{33+25}=\sqrt{58}[/math], так как [math]A_1B_1=AB[/math]. В прямоугольном треугольнике [math]AA_1B[/math] по теореме Пифагора [math]A_1B=\sqrt{AB^2+AA_1^2}=\sqrt{256+33}=17[/math]. [math]\cos\angle HBA_1=\frac{HB}{A_1B}=\frac{\sqrt{58}}{17}[/math]
Ответ: [math]\frac{\sqrt{58}}{17}[/math]
Решите систему неравенств [math]\left\{\begin{array}{l}25^\frac x2+\frac{20}{5^x}\geq9,\\\log_{x+5}\left(\frac{x+2}5\right)\leq0.\end{array}\right.[/math]
Решение:
1) [math]5^x+\frac{20}{5^x}-9\geq0.[/math]
[math]\frac{(5^x)^2-9\times5^x+20}{5^x}\geq0,\;5^x=t,\;t>0[/math]
[math]\frac{t^2-9t+20}t\geq0[/math]
[math]\frac{(t-4)(t-5)}t\geq0[/math]
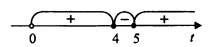
[math]0<t\leq4;\;t\geq5[/math]
[math]0<5^x\leq5^{\log_54};\;5^x\geq5^1[/math]
[math]x\leq\log_54;\;x\geq1[/math]
2) [math]\log_{x+5}(\frac{x+2}5)\leq\log_{x+5}1[/math]
ОДЗ: [math]\left\{\begin{array}{l}x+5>0\\x+5\neq1\\x+2>0\end{array}\right.[/math] [math]x>-2[/math]
На ОДЗ выражение [math]\log_{x+5}(\frac{x+2}5)-\log_{x+5}1[/math] совпадает по знаку с выражением (x+5-1)(x/5+0,4-1).
Получим [math](x+4)(x-3)\leq0[/math]
[math]-4\leq x\leq3[/math] с учетом ОДЗ получаем: [math]-2<x\leq3[/math]
3) Решим систему [math]\left\{\begin{array}{l}x\leq\log_54,\;x\geq1\\-2<x\leq3\end{array}\right.\;\;\left\{\begin{array}{l}-2<x\leq\log_54\\1\leq x\leq3\end{array}\right.[/math]
Ответ: [math]\;(-2;\log_54\rbrack,\lbrack1;3\rbrack.[/math]
Диагонали АС и BD трапеции ABCD взаимно перпендикулярны и пересекаются в точке О, причём АО • СО = ВО • DO.
а) Докажите, что трапеция ABCD равнобедренная.
б) Найдите радиус описанной вокруг трапеции окружности, если основания трапеции равны 6 и 8.
Решение:
а) В трапеции [math]ABCD[/math] треугольники [math]AOD[/math] и [math]BOC[/math] подобны, поскольку [math]\angle OAD=\angle OCB[/math] и [math]\angle ODA=\angle OBC[/math] как накрест лежащие при параллельных прямых [math]AD[/math] и [math]BC[/math] и секущих [math]AC[/math] и [math]BD[/math] соответственно (см. рисунок)
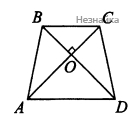
Значит, [math]\frac{AO}{CO}=\frac{DO}{BO}[/math]. Умножая почленно это равенство на равенство [math]AO\times CO=BO\times DO[/math] из условия задачи, получим [math]AO^2=DO^2[/math]. Отсюда [math]AO=DO[/math], [math]BO=CO[/math] и треугольники [math]AOB[/math] и [math]DOC[/math] равны по первому признаку. Следовательно [math]AB=CD[/math]
б) Т.к. Трапеция [math]ABCD[/math] равнобедренная, то вокруг нее можно описать окружность. обозначим ее радиус через [math]R[/math].
Треугольники [math]AOD[/math] и [math]BOC[/math] - равнобедренные и прямоугольные. Значит [math]\angle OAD=45^\circ[/math] и [math]CO=\frac{BC}{\sqrt2}[/math], [math]DO=\frac{AD}{\sqrt2}[/math]. По теореме синусов для треугольника ACD имеем: [math]\frac{CD}{\sin\angle CAD}=2R,\;R=\frac{CD}{\sqrt2}[/math]
[math]CD^2=CO^2+DO^2=\frac12(AD^2+BC^2)=50[/math]
Отсюда [math]CD=5\sqrt2[/math] и R=5
Ответ: 5
Заводы в США и России за февраль выпустили более 39 танков. Число танков, выпущенных в России, уменьшенное на 3, более чем в 4 раза превышает число танков, выпущенных в США. Утроенное число танков, выпущенных в России, превышает удвоенное число танков, выпущенных за февраль в США, но не более, чем на 85. Сколько танков выпустили за февраль на заводе в России?
Решение:
Пусть за февраль на заводе в России выпустили [math]x[/math] танков, а в США - [math]y[/math] танков. По условию можно составить систему неравенств:
[math]\left\{\begin{array}{l}\begin{array}{c}x+y>39\\x-3>4y\end{array}\\3x-2y\leq85\end{array}\right.[/math]
При этом [math]x[/math] и [math]y[/math] - натуральные числа. Выразим одну из переменных во всех трех неравенствах:
[math]\left\{\begin{array}{l}\begin{array}{c}x>39-y\\x>4y+3\end{array}\\x\leq\frac{85+2y}3\end{array}\right.[/math]
[math]\left\{\begin{array}{l}39-y<x\leq\frac{85+2y}3\\4y+3<x\leq\frac{85+2y}3\end{array}\right.[/math]
[math]\left\{\begin{array}{l}117-3y<85+2y\\12y+9<85+2y\end{array}\right.[/math]
[math]\left\{\begin{array}{l}y>6,4\\y<7,6\end{array}\right.[/math]
[math]y=7[/math] - единственное целое решение. Подставим его в начальную систему неравенств
[math]\left\{\begin{array}{l}\begin{array}{c}x+7>39\\x-3>28\end{array}\\3x-14\leq85\end{array}\right.[/math]
Так как [math]x[/math] - целое, то [math]x=33[/math]. В России на заводе за февраль выпустили 33 танка.
Ответ: 33
Найдите все значения а, при которых любое решение уравнения [math]6\sqrt{x-1}+5\log_3(2x-1)+11a=0[/math] принадлежит отрезку [2 ; 5]
Решение:
Рассмотрим функцию [math]f(x)=6\sqrt{x-1}+5\log_3(2x-1).[/math] Она определена при [math]x\geq1[/math] и возрастает на всей области определения. Значит уравнение [math]f(x)+11a=0[/math] может иметь единственное решение (при соответствующих значениях параметра a). Это решение принадлежит отрезку [math]\left[2;5\right][/math] тогда и только тогда, когда:
[math]\left\{\begin{array}{l}6+5+11a\leq0\\12+10+11a\geq0\end{array}\right.[/math], откуда:
[math]-2\leq a\leq-1[/math]
Ответ: [math]\left[-2;-1\right][/math]
а) Можно ли число 2015 представить в виде суммы трёх различных натуральных чисел с одинаковой суммой цифр?
б) Можно ли число 288 представить в виде суммы трёх различных натуральных чисел с одинаковой суммой цифр?
в) Найдите наименьшее натуральное число, которое можно представить в виде суммы шести различных натуральных чисел с одинаковой суммой цифр.
Решение:
а) Нет. Справедлив обобщенный признак делимости на 3, а именно: "Натуральное число дает при делении на 3 тот же остаток, что и сумма его цифр." Тогда сумма трех чисел с одинаковой суммой цифр будет обязательно делиться на 3, поскольку все эти числа будут давать один и тот же остаток при делении на 3. Но 2015 на 3 нацело не делится.
б) Да. Например, 288=240+33+15
в) Пусть шесть различных натуральных чисел имеют одинаковую сумму цифр. Тогда все они дают один и тот же остаток при делании на 9 и разность любых двух из них будет кратна 9 (и не может равняться 0). Это значит, что эти числа будут членами некоторой арифметической прогрессии с разностью [math]d=9[/math] (не обязательно последовательными)
наименьшее значение сумма данных чисел будет принимать в том случае, если у каждого из чисел будет минимально возможная разрядность (5 предпочтительнее с этой точки зрения, например, чем 14, а 14, в свою очередь, предпочтительнее, например, чем 302). Тогда наименьшею сумму будут давать те числа, которые являются последовательными членами арифметической прогрессии с разностью [math]d=9[/math], начиная с однозначного (равного соответствующему остатку при делении на 9).
Сумма цифр равна 1:1+10 +100+1000+10000+100000=111111.
Сумма цифр равна 2: 2+11+20+101+110+200=444
Сумма цифр равна 3: 3+12+21+30+102+111=279
Сумма цифр равна 4: 4+13+22+31+40+103=213
Сумма цифр равна 5: 5+14+23+32+41+50=165
Сумма цифр равна 6: 6+15+24+33+42+51=171
Дальше сумма будет только возрастать, т.к. [math]r[/math] - наименьшее из данных чисел, то сумма всех шести будет не меньше
[math]r+(r+9)+(r+18)+(r+27)+(r+36)+(r+45)=6r+135>165[/math] при [math]r\geq6[/math]
Итак, наименьшим числом, которое можно представить в виде шести различных натуральных чисел с одинаковой суммой цифр является 165
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||