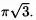
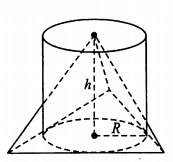
Начнем с того, что знаем: [math]V_ц=\mathrm{πR}^2\times\mathrm h[/math];

и что надо найти: [math]V_п=\frac13\times h\times S_{осн}[/math], где [math]S_{осн}=\frac{а^2\sqrt3}4[/math], а - сторона правильного треугольника в основании.

[math]V_п=\frac{\sqrt3}{12}h\times a^2[/math]

Остается добавить связь стороны правильного треугольника с радиусом вписанной окружности: [math]R=\frac{\sqrt3}6a[/math]

Подставляя последнее выражение в формулу объема цилиндра, получается: [math]V_ц=\frac{\mathrm\pi}{12}a^2\times h[/math]

Теперь возьмем отношение объемов [math]\frac{V_п}{V_ц}=\frac{{\displaystyle\frac{\sqrt3}{12}}h\times a^2}{{\displaystyle\frac{\mathrm\pi}{12}}a^2\times h}=\frac{\sqrt3}{\mathrm\pi}[/math]

[math]V_п=\frac{\sqrt3}{\mathrm\pi}V_ц=\frac{\sqrt3}{\mathrm\pi}\times\mathrm\pi\sqrt3=3[/math]