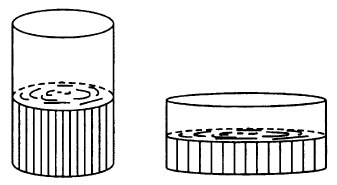
Объём цилиндра рассчитывается так: высота цилиндра помножить на площадь основания, т.е. площадь круга. Пока условно посчитаем объем: [math]V=\pi R^2\times h=27\pi R^2[/math].

Речь идет о жидкости, у которой объем постоянен. Т.е. для того же объема рассчитывается цилиндр, но уже с радиусом основания в 3 раза больше и с неизвестным уровнем жидкости: [math]V=\mathrm\pi\left(3\mathrm R\right)^2\times\mathrm H=9\mathrm{πR}^2\times\mathrm H[/math]

[math]\begin{array}{l}27\mathrm{πR}^2=9\mathrm{πR}^2\times\mathrm H\\\mathrm H=\frac{27}9=3\end{array}[/math]

Т.е. уровень воды будет находиться на уровне [math]H=3[/math]