Задание № 26594
Постройте график функции [math]y=\frac{(x^2+6,25)(x-1)}{1-x}[/math] и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
Область определения: x≠1 [math]y=\frac{(x^2+6,25)(x-1)}{1-x}[/math] - сокращаем дробь y=-x2-6,25 - парабола, ветви вниз, вершина (0;-6,25)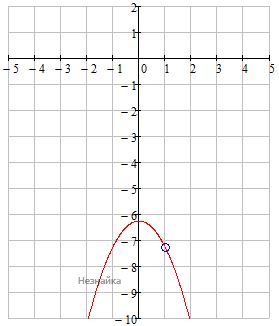 Прямая y=kx имеет с графиком ровно одну общую точку, при таких k, при которых данное уравнение имеет один корень:
-x2-6,25=kx
x2-kx+6,25=0
D=k2-4•6,25=0
k2-4•6,25=0
k2=25
k=±5
А так же при пересечении прямой y=kx графика функции в точке х=1:
y=-12-6,25=-7,25
y=kx → -7,25=k•1
k=-7,25
Ответ: -7,25;-5;5
Ответ:
Прямая y=kx имеет с графиком ровно одну общую точку, при таких k, при которых данное уравнение имеет один корень:
-x2-6,25=kx
x2-kx+6,25=0
D=k2-4•6,25=0
k2-4•6,25=0
k2=25
k=±5
А так же при пересечении прямой y=kx графика функции в точке х=1:
y=-12-6,25=-7,25
y=kx → -7,25=k•1
k=-7,25
Ответ: -7,25;-5;5
Ответ:
Область определения: x≠1 [math]y=\frac{(x^2+6,25)(x-1)}{1-x}[/math] - сокращаем дробь y=-x2-6,25 - парабола, ветви вниз, вершина (0;-6,25)
 Прямая y=kx имеет с графиком ровно одну общую точку, при таких k, при которых данное уравнение имеет один корень:
-x2-6,25=kx
x2-kx+6,25=0
D=k2-4•6,25=0
k2-4•6,25=0
k2=25
k=±5
А так же при пересечении прямой y=kx графика функции в точке х=1:
y=-12-6,25=-7,25
y=kx → -7,25=k•1
k=-7,25
Ответ: -7,25;-5;5
Ответ:
Прямая y=kx имеет с графиком ровно одну общую точку, при таких k, при которых данное уравнение имеет один корень:
-x2-6,25=kx
x2-kx+6,25=0
D=k2-4•6,25=0
k2-4•6,25=0
k2=25
k=±5
А так же при пересечении прямой y=kx графика функции в точке х=1:
y=-12-6,25=-7,25
y=kx → -7,25=k•1
k=-7,25
Ответ: -7,25;-5;5
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.