Вариант 10
Часть 1.
Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.
Прочитайте внимательно текст и выполните задания 1–5
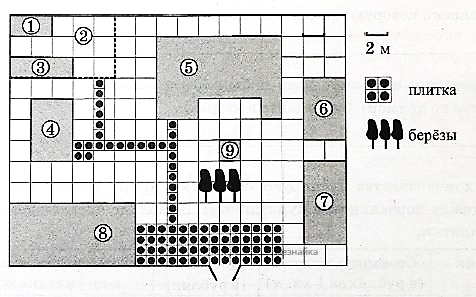
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.
Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.
| Объекты | курятник | теплица | коровник | огород | баня |
| Цифры |
Тротуарная плитка продаётся в упаковках по 20 штук. Сколько упаковок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?
Найдите площадь, которую суммарно занимают коровник и курятник. Ответ дайте в квадратных метрах.
Найдите расстояние от теплица до компостной ямы (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.
Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трёх поставщиков плитки. Рассчитайте самый выгодный вариант и запишите его в ответ.
| Поставщик | Стоимость плитки (в руб. за 1 кв.м.) | Доставка (в руб.) | Работы по демонтажу старой плитки и по укладке новой (в руб.) |
| 1 | 255 | 1200 | 8000 |
| 2 | 260 | 1300 | 6000 |
| 3 | 280 | бесплатно | 4000 |
Найдите значение выражения
[math]\frac{256\cdot10^3}{3200}\div20+\frac25[/math]
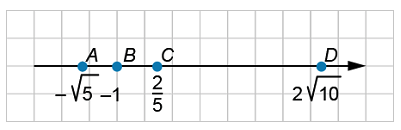
Сколько целых чисел находится в промежутке между точками A и C?
Значение какого из выражений является рациональным числом?
1) [math](\sqrt5-2)\cdot(\sqrt2-5)[/math]
2) [math](\sqrt2+5)\cdot(2+\sqrt5)[/math]
3) [math](\sqrt5-2)\cdot(2+\sqrt5)[/math]
4) [math](\sqrt2+5)\cdot(2-\sqrt5)[/math]
Найдите корни уравнения [math]x^3-16x=0[/math]. В ответе укажите его наименьший корень.
В личной библиотеке Маши 50 книг. 20 из них приключенческих, 25 — художественные, остальные — фэнтези. Петя пришел в гости к Маше и взял с полки наугад одну книгу. С какой вероятностью книга окажется в жанре фэнтези?
На рисунке изображен график функции [math]y=ax^2+bx+c[/math]
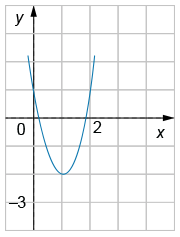
Определите с помощью графика значение выражения [math]5-\frac ba[/math]
Последовательность чисел задана условием:
[math]b_{10}=-2[/math], [math]b_n=b_{n-1}+3[/math], [math]n>1[/math]. Найдите сумму первых пяти членов последовательности [math]b_n[/math]
Найдите значение выражения
[math]\frac{v^2-x^2}{v^2+x^2+2vx}\div\frac{x-v}2[/math], если [math]x=2+\sqrt5[/math], [math]v=2-\sqrt5[/math]
Кинетическая энергия движущегося тела определяется по формуле [math]E_k=\frac{mv^2}2[/math], где [math]E_k[/math] (в Дж) — кинетическая энергия, m (в кг) — масса тела, а v (в м/с) — его скорость. Найдите кинетическую энергию голубя массой 0,35 кг, летящего со скоростью 54 км/ч.
Решите неравенство [math]\frac1{(2x+3)^2}\geq4[/math]
1) [1,25; 1,75]
2) [−1,75; −1,25]
3) [−1,75; −1,5) ∪ (−1,5; −1,25]
4) [1,25; 1,5) ∪ (1,5; 1,75]
В равностороннем треугольнике ABC проведена медиана AM. Сторона AB=10 см. Чему равен отрезок MB (в см)?
В четырехугольник ABCD вписана окружность. Периметр четырехугольника равен 120 см, сторона CD=20 см. Найдите сторону AB. Ответ дайте в см.
Найдите площадь трапеции, средняя линия которой равна 6 см, а высота — 5 см. Ответ дайте в см2
Найдите тангенс угла ABC, изображённого на рисунке.
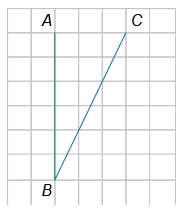
Укажите номера верных утверждений. Выберите 2 варианта из списка.
1) Диагонали ромба равны.
2) Любой прямоугольник является параллелограммом.
3) Косинус угла в треугольнике всегда меньше синуса.
4) Все высоты треугольника пересекаются в одной точке.
Часть 2.
При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Решите систему уравнений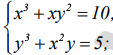 
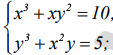1) [math]\{\begin{array}{c}x(x^2+y^2)=10\\y(x^2+y^2)=5\end{array}[/math] [math]\frac{x(x^2+y^2)}{y(x^2+y^2)}=\frac{10}5[/math] [math]\frac xy=2[/math] x=2y 2) x3+xy2=10 (2y)3+(2y)y2=10 8y3+2y3=10 10y3=10 y3=1 y=1 x=2y=2 Ответ: (2;1)Дорога между пунктами А и В, длиной 36 км, состоит из подъёма и спуска. Велосипедист, двигаясь на спуске со скоростью на 6 км/ч большей, чем на подъёме, затрачивает на путь из А в В 2 ч 40 мин, а на обратный путь на 20 мин меньше. Найдите скорость велосипедиста на подъёме и на спуске.
Постройте график функции [math]y=\frac{(x^2+6,25)(x-1)}{1-x}[/math] и определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
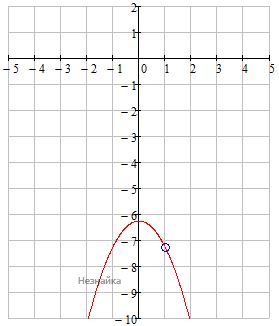Прямая y=kx имеет с графиком ровно одну общую точку, при таких k, при которых данное уравнение имеет один корень: -x2-6,25=kx x2-kx+6,25=0 D=k2-4•6,25=0 k2-4•6,25=0 k2=25 k=±5 А так же при пересечении прямой y=kx графика функции в точке х=1: y=-12-6,25=-7,25 y=kx → -7,25=k•1 k=-7,25 Ответ: -7,25;-5;5Углы, образуемые диагоналями ромба с одной из его сторон относятся как 2:3. Найдите углы ромба
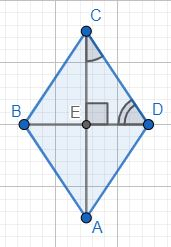Согласно условию: ∠ECD/∠EDC=2/3 → ∠ECD=∠EDC•2/3. Диагонали ромба взаимно перпендикулярны. Сумма острых углов в прямоугольном треугольнике △ECD равна 90°: ∠ECD+∠EDC=90° ∠EDC•2/3+∠EDC=90° ∠EDC•2/3+∠EDC=90° ∠EDC•5/3=90° ∠EDC=54° ∠ECD=∠EDC•2/3=54°•2/3=36° Диагонали ромба являются биссектрисами его углов: ∠С=∠А=2•∠ECD=2•36°=72° ∠D=∠B=2•∠EDC=2•54°=108° Ответ: 72;108Докажите, что в прямоугольном треугольнике сумма катетов равна сумме диаметров вписанной и описанной окружностей.
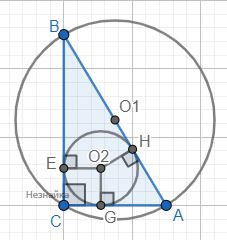R и r – радиусы соответственно описанной и вписанной окружностей прямоугольного треугольника ABC с прямым углом C. Гипотенуза – диаметр описанной окружности, поэтому AB=2R. Если O2 – центр вписаннной окружности, то O2GCE – квадрат. Тогда EC=GC=r, AG=AH=AC-GC, BE=BH=BC-EC. 2R=AB=AH+BH=AC-GC+BC-EC=AC+BC-2r 2R=AC+BC-2r 2R+2r=AC+BCВ прямоугольном треугольнике ABC проведена биссектриса ВЕ, а на гипотенузе ВС взята точка М так, что ЕМ [math]\perp[/math] ВЕ. Найдите площадь треугольника АВС, если СМ=1, СЕ=2.
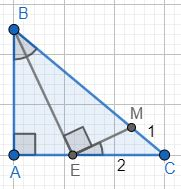1)Так как BE - биссектриса, то ∠EBA=∠EBM. В △BEA: ∠BEA=90°-∠EBA. Тогда: ∠CEM=180°-∠BEA-∠BEM=180°-(90°-∠EBA)-90°=∠EBA=∠EBM Треугольники △EMC~△BEC подобны по двум углам ∠C-общий, ∠CEM=∠EBM. Значит: [math]\frac{MC}{EC}=\frac{EC}{BC}[/math] [math]\frac12=\frac2{BC}[/math] BC=4 2) По свойству биссектрисы [math]\frac{AE}{EC}=\frac{AB}{BC}[/math] [math]\frac{AE}2=\frac{AB}4[/math] AB=2AE 3) По теореме Пифагора △ABC: BC2=AB2+AC2 BC2=AB2+(AE+EC)2 42=(2AE)2+(AE+2)2 16=4AE2+AE2+4AE+4 5AE2+4AE-12=0 D=42-4•5•(-12)=256 [math]AE_1=\frac{-4-\sqrt{256}}{2\cdot5}=-2[/math] - неудовлетворяет условию задачи [math]AE_2=\frac{-4+\sqrt{256}}{2\cdot5}=1,2[/math] 4) AB=2AE=2•1,2=2,4 AC=AE+EC=1,2+2=3,2 S=3,2•2,4/2=3,84 Ответ: 3,84| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||