Задание № 26571
В прямоугольном треугольнике АВС точки D и E лежат соответственно на катетах BC и AC так, что CD = CE = 1. Точка M — точка пересечения отрезков AD и BE Площадь треугольника BMD больше площади треугольника AME на 1/2. Известно, что AD = √10. Найдите длину гипотенузы AB.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
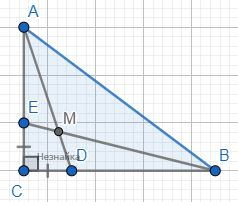 1) По теореме Пифагора △ACD:
AC2+CD2=AD2
AC2+12=√102
AC2=9
AC=3
2) S△BMD-S△AME=1/2
Добавим и вычтем SEMDC
S△BMD+SEMDC-S△AME-SEMDC=1/2
S△BEC=S△BMD+SEMDC=BC•CE/2=BC/2
S△ADC=S△AME+SEMDC=AC•CD/2=3/2
S△BEC-S△ADC=1/2
BC/2 - 3/2 = 1/2
BC-3=1
BC=4
3) По теореме Пифагора △ABC:
AB=√(AC2+BC2)=√(32+42)=5
Ответ: 5
Ответ:
1) По теореме Пифагора △ACD:
AC2+CD2=AD2
AC2+12=√102
AC2=9
AC=3
2) S△BMD-S△AME=1/2
Добавим и вычтем SEMDC
S△BMD+SEMDC-S△AME-SEMDC=1/2
S△BEC=S△BMD+SEMDC=BC•CE/2=BC/2
S△ADC=S△AME+SEMDC=AC•CD/2=3/2
S△BEC-S△ADC=1/2
BC/2 - 3/2 = 1/2
BC-3=1
BC=4
3) По теореме Пифагора △ABC:
AB=√(AC2+BC2)=√(32+42)=5
Ответ: 5
Ответ:
 1) По теореме Пифагора △ACD:
AC2+CD2=AD2
AC2+12=√102
AC2=9
AC=3
2) S△BMD-S△AME=1/2
Добавим и вычтем SEMDC
S△BMD+SEMDC-S△AME-SEMDC=1/2
S△BEC=S△BMD+SEMDC=BC•CE/2=BC/2
S△ADC=S△AME+SEMDC=AC•CD/2=3/2
S△BEC-S△ADC=1/2
BC/2 - 3/2 = 1/2
BC-3=1
BC=4
3) По теореме Пифагора △ABC:
AB=√(AC2+BC2)=√(32+42)=5
Ответ: 5
Ответ:
1) По теореме Пифагора △ACD:
AC2+CD2=AD2
AC2+12=√102
AC2=9
AC=3
2) S△BMD-S△AME=1/2
Добавим и вычтем SEMDC
S△BMD+SEMDC-S△AME-SEMDC=1/2
S△BEC=S△BMD+SEMDC=BC•CE/2=BC/2
S△ADC=S△AME+SEMDC=AC•CD/2=3/2
S△BEC-S△ADC=1/2
BC/2 - 3/2 = 1/2
BC-3=1
BC=4
3) По теореме Пифагора △ABC:
AB=√(AC2+BC2)=√(32+42)=5
Ответ: 5
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.