Задание № 26568
Постройте график функции [math]y=x^2-4\vert x\vert-x[/math] и определите, при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
у=х2-4|х|-х Раскроем знак модуля 1) При х<0 у=х2-4(-х)-х у=х2+3х у=х2+3х=х2+3х+1,52-1,52=(х+1,5)-2,25 - парабола, ветви вверх, вершина (-1,5;-2,25)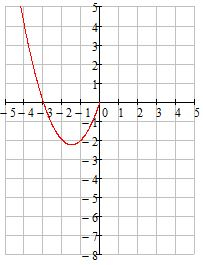 2) При х≥0
у=х2-4х-х
у=х2-5х
у=х2-5х=х2-5х+2,52-2,52=(х-2,5)-6,25 - парабола, ветви вверх, вершина (2,5;-6,25)
2) При х≥0
у=х2-4х-х
у=х2-5х
у=х2-5х=х2-5х+2,52-2,52=(х-2,5)-6,25 - парабола, ветви вверх, вершина (2,5;-6,25)
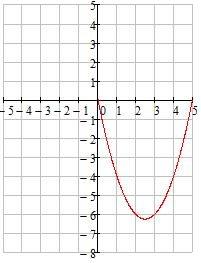 3) Совмещаем оба графика и определяем при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
3) Совмещаем оба графика и определяем при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
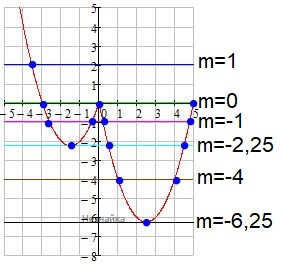 При mє(0;∞) прямая y=m и график функции имеют 2 общие точки
При m=0 и m=-2,25 прямая y=m и график функции имеют 3 общие точки
При mє(-6,25;-2,25) прямая y=m и график функции имеют 2 общие точки
При m=-6,25 прямая y=m и график функции имеют 1 общую точку
Ответ: [-6,25;-2,25], [0;∞)
Ответ:
При mє(0;∞) прямая y=m и график функции имеют 2 общие точки
При m=0 и m=-2,25 прямая y=m и график функции имеют 3 общие точки
При mє(-6,25;-2,25) прямая y=m и график функции имеют 2 общие точки
При m=-6,25 прямая y=m и график функции имеют 1 общую точку
Ответ: [-6,25;-2,25], [0;∞)
Ответ:
у=х2-4|х|-х Раскроем знак модуля 1) При х<0 у=х2-4(-х)-х у=х2+3х у=х2+3х=х2+3х+1,52-1,52=(х+1,5)-2,25 - парабола, ветви вверх, вершина (-1,5;-2,25)
 2) При х≥0
у=х2-4х-х
у=х2-5х
у=х2-5х=х2-5х+2,52-2,52=(х-2,5)-6,25 - парабола, ветви вверх, вершина (2,5;-6,25)
2) При х≥0
у=х2-4х-х
у=х2-5х
у=х2-5х=х2-5х+2,52-2,52=(х-2,5)-6,25 - парабола, ветви вверх, вершина (2,5;-6,25)
 3) Совмещаем оба графика и определяем при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
3) Совмещаем оба графика и определяем при каких значениях m прямая y=m имеет с графиком не менее одной, но не более трёх общих точек.
 При mє(0;∞) прямая y=m и график функции имеют 2 общие точки
При m=0 и m=-2,25 прямая y=m и график функции имеют 3 общие точки
При mє(-6,25;-2,25) прямая y=m и график функции имеют 2 общие точки
При m=-6,25 прямая y=m и график функции имеют 1 общую точку
Ответ: [-6,25;-2,25], [0;∞)
Ответ:
При mє(0;∞) прямая y=m и график функции имеют 2 общие точки
При m=0 и m=-2,25 прямая y=m и график функции имеют 3 общие точки
При mє(-6,25;-2,25) прямая y=m и график функции имеют 2 общие точки
При m=-6,25 прямая y=m и график функции имеют 1 общую точку
Ответ: [-6,25;-2,25], [0;∞)
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.