Задание № 26545
В параллелограмме ABCD угол А равен 80°, сторона АВ равна 7. Биссектриса угла при вершине А пересекает сторону CD в точке Е. Найдите радиус окружности, касающейся отрезка АВ и лучей ВС и АЕ.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
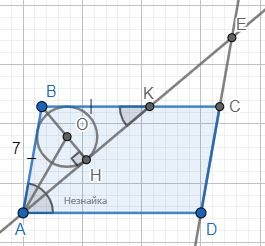 Биссектриса AE пересекает BC в точке K. Углы ∠BKA=∠DAE - как накрест лежащие, ∠BAK=∠DAE - AE биссектриса, следовательно, ∠BKA=∠BAK, значит △ABK равнобедренный. Тогда AB=BK=7 и ∠BKA=∠BAK=40°
Центр вписанной окружности - точка пересечения биссектрис. Проведем AO биссектрису ∠BAH и BH высоту △ABK → OH - радиус окружности.
Треугольник △ABH прямоугольный:
[math]cos\angle HAB=\frac{AH}{AB}\rightarrow AH=ABcos\angle HAB[/math]
Треугольник △AOH прямоугольный
[math]tg\angle HAO=\frac{OH}{AH}[/math]
[math]OH=AHtg\angle HAO=ABcos\angle HABtg\angle HAO=7cos40^\circ tg20^\circ[/math]
Ответ: 7cos40° tg20°
Ответ:
Биссектриса AE пересекает BC в точке K. Углы ∠BKA=∠DAE - как накрест лежащие, ∠BAK=∠DAE - AE биссектриса, следовательно, ∠BKA=∠BAK, значит △ABK равнобедренный. Тогда AB=BK=7 и ∠BKA=∠BAK=40°
Центр вписанной окружности - точка пересечения биссектрис. Проведем AO биссектрису ∠BAH и BH высоту △ABK → OH - радиус окружности.
Треугольник △ABH прямоугольный:
[math]cos\angle HAB=\frac{AH}{AB}\rightarrow AH=ABcos\angle HAB[/math]
Треугольник △AOH прямоугольный
[math]tg\angle HAO=\frac{OH}{AH}[/math]
[math]OH=AHtg\angle HAO=ABcos\angle HABtg\angle HAO=7cos40^\circ tg20^\circ[/math]
Ответ: 7cos40° tg20°
Ответ:
 Биссектриса AE пересекает BC в точке K. Углы ∠BKA=∠DAE - как накрест лежащие, ∠BAK=∠DAE - AE биссектриса, следовательно, ∠BKA=∠BAK, значит △ABK равнобедренный. Тогда AB=BK=7 и ∠BKA=∠BAK=40°
Центр вписанной окружности - точка пересечения биссектрис. Проведем AO биссектрису ∠BAH и BH высоту △ABK → OH - радиус окружности.
Треугольник △ABH прямоугольный:
[math]cos\angle HAB=\frac{AH}{AB}\rightarrow AH=ABcos\angle HAB[/math]
Треугольник △AOH прямоугольный
[math]tg\angle HAO=\frac{OH}{AH}[/math]
[math]OH=AHtg\angle HAO=ABcos\angle HABtg\angle HAO=7cos40^\circ tg20^\circ[/math]
Ответ: 7cos40° tg20°
Ответ:
Биссектриса AE пересекает BC в точке K. Углы ∠BKA=∠DAE - как накрест лежащие, ∠BAK=∠DAE - AE биссектриса, следовательно, ∠BKA=∠BAK, значит △ABK равнобедренный. Тогда AB=BK=7 и ∠BKA=∠BAK=40°
Центр вписанной окружности - точка пересечения биссектрис. Проведем AO биссектрису ∠BAH и BH высоту △ABK → OH - радиус окружности.
Треугольник △ABH прямоугольный:
[math]cos\angle HAB=\frac{AH}{AB}\rightarrow AH=ABcos\angle HAB[/math]
Треугольник △AOH прямоугольный
[math]tg\angle HAO=\frac{OH}{AH}[/math]
[math]OH=AHtg\angle HAO=ABcos\angle HABtg\angle HAO=7cos40^\circ tg20^\circ[/math]
Ответ: 7cos40° tg20°
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.