Задание № 26543
В треугольник АВС вписана окружность с центром в точке О. Луч АО пересекает сторону ВС в точке К. Найдите площадь треугольника АВС, если АВ=13, АС=15, ВК=6,5.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
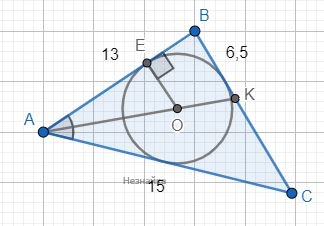Центром окружности вписанной в треугольник, является точка пересечения биссектрис. Следовательно АК - биссектриса.
По свойству биссектрисы:
[math]\frac{CK}{BK}=\frac{AC}{AB}[/math]
[math]CK=\frac{AC}{AB}\cdot BK=\frac{15}{13}\cdot6,5=7,5[/math]
ВС=ВК+СК=6,5+7,5=14
По формуле Герона:
[math]p=\frac{AB+BC+AC}2=\frac{13+14+15}2=21[/math]
[math]S=\sqrt{p(p-AC)(p-AB)(p-BC)}=\sqrt{21\cdot(21-13)(21-14)(21-15)}=[/math]
[math]=\sqrt{21\cdot8\cdot7\cdot6}=\sqrt{7\cdot3\cdot2\cdot2\cdot2\cdot7\cdot2\cdot3}=7\cdot3\cdot2\cdot2=84[/math]
Ответ: 84
Ответ:
Центром окружности вписанной в треугольник, является точка пересечения биссектрис. Следовательно АК - биссектриса.
По свойству биссектрисы:
[math]\frac{CK}{BK}=\frac{AC}{AB}[/math]
[math]CK=\frac{AC}{AB}\cdot BK=\frac{15}{13}\cdot6,5=7,5[/math]
ВС=ВК+СК=6,5+7,5=14
По формуле Герона:
[math]p=\frac{AB+BC+AC}2=\frac{13+14+15}2=21[/math]
[math]S=\sqrt{p(p-AC)(p-AB)(p-BC)}=\sqrt{21\cdot(21-13)(21-14)(21-15)}=[/math]
[math]=\sqrt{21\cdot8\cdot7\cdot6}=\sqrt{7\cdot3\cdot2\cdot2\cdot2\cdot7\cdot2\cdot3}=7\cdot3\cdot2\cdot2=84[/math]
Ответ: 84
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.