Задание № 26517
Площадь равнобедренной трапеции равна 96. Диагональ трапеции делит её тупой угол пополам. Длина меньшего основания равна 3. Найдите периметр трапеции.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
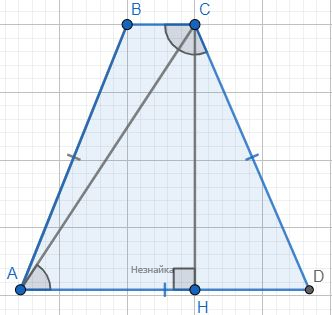 Если диагональ трапеции делит её тупой угол пополам. то ∠ACB=∠ACD.
∠ABC=∠DAC - как накрест лежащие. Значит ∠ACB=∠ACD=∠DAC, следовательно △DAC - равнобедренный → AD=CD=AB=Х так как трапеция равнобедренная.
DH=(BC-AD)/2=(3-Х)/2
По теореме Пифагора в треугольнике △DCH:
CH2=CD2-DH2
[math]CH=\sqrt{X^2-\left(\frac{3-X}2\right)^2}=\sqrt{X^2-\frac94+\frac{3X}2-\frac{X^2}4}=\sqrt{\frac34X^2+\frac32X-\frac94}=\frac12\sqrt{3X^2+6X-9}[/math]
Площадь трапеции:
[math]S=\frac{BC+AD}2CH=\frac{3+X}2\cdot\frac12\sqrt{3X^2+6X-9}=96[/math]
Получаем уравнение:
[math]\frac{3+X}4\sqrt{3X^2+6X-9}=96[/math]
[math]\sqrt{3X^2+6X-9}=\frac{384}{3+X}[/math]
Возведем обе части уравнения в квадрат, так как они обе положительные:
[math]\left(\sqrt{3X^2+6X-9}\right)^2=\left(\frac{384}{3+X}\right)^2[/math]
[math]3X^2+6X-9=\frac{147556}{9+6X+X^2}[/math]
[math]\left(3X^2+6X-9\right)\left(X^2+6X+9\right)=147556[/math]
[math]3X^4+24X^3+54X^2-147537=0[/math]
X4+8X3+18X2-49179=0
Корни данного уравнения находятся среди множителей числа 49179=13•13•9•97
Разделим многочлен (X4+8X3+18X2-49179) на (X-13)
[math]\frac{X^4+8X^3+18X^2-49179}{X-13}=X^3+21X^2+291X+3783[/math]
Значит X=13 один из корней уравнения X4+8X3+18X2-49179=0
Решения уравнения X3+21X2+291X+3783=0 являются отрицательными или комплексными числами, которые условию задачи не удовлетворяют.
AD=CD=AB=Х=13
P=AD+CD+AB+BC=13+13+13+3=42
Ответ: 42
Ответ:
Если диагональ трапеции делит её тупой угол пополам. то ∠ACB=∠ACD.
∠ABC=∠DAC - как накрест лежащие. Значит ∠ACB=∠ACD=∠DAC, следовательно △DAC - равнобедренный → AD=CD=AB=Х так как трапеция равнобедренная.
DH=(BC-AD)/2=(3-Х)/2
По теореме Пифагора в треугольнике △DCH:
CH2=CD2-DH2
[math]CH=\sqrt{X^2-\left(\frac{3-X}2\right)^2}=\sqrt{X^2-\frac94+\frac{3X}2-\frac{X^2}4}=\sqrt{\frac34X^2+\frac32X-\frac94}=\frac12\sqrt{3X^2+6X-9}[/math]
Площадь трапеции:
[math]S=\frac{BC+AD}2CH=\frac{3+X}2\cdot\frac12\sqrt{3X^2+6X-9}=96[/math]
Получаем уравнение:
[math]\frac{3+X}4\sqrt{3X^2+6X-9}=96[/math]
[math]\sqrt{3X^2+6X-9}=\frac{384}{3+X}[/math]
Возведем обе части уравнения в квадрат, так как они обе положительные:
[math]\left(\sqrt{3X^2+6X-9}\right)^2=\left(\frac{384}{3+X}\right)^2[/math]
[math]3X^2+6X-9=\frac{147556}{9+6X+X^2}[/math]
[math]\left(3X^2+6X-9\right)\left(X^2+6X+9\right)=147556[/math]
[math]3X^4+24X^3+54X^2-147537=0[/math]
X4+8X3+18X2-49179=0
Корни данного уравнения находятся среди множителей числа 49179=13•13•9•97
Разделим многочлен (X4+8X3+18X2-49179) на (X-13)
[math]\frac{X^4+8X^3+18X^2-49179}{X-13}=X^3+21X^2+291X+3783[/math]
Значит X=13 один из корней уравнения X4+8X3+18X2-49179=0
Решения уравнения X3+21X2+291X+3783=0 являются отрицательными или комплексными числами, которые условию задачи не удовлетворяют.
AD=CD=AB=Х=13
P=AD+CD+AB+BC=13+13+13+3=42
Ответ: 42
Ответ:
 Если диагональ трапеции делит её тупой угол пополам. то ∠ACB=∠ACD.
∠ABC=∠DAC - как накрест лежащие. Значит ∠ACB=∠ACD=∠DAC, следовательно △DAC - равнобедренный → AD=CD=AB=Х так как трапеция равнобедренная.
DH=(BC-AD)/2=(3-Х)/2
По теореме Пифагора в треугольнике △DCH:
CH2=CD2-DH2
[math]CH=\sqrt{X^2-\left(\frac{3-X}2\right)^2}=\sqrt{X^2-\frac94+\frac{3X}2-\frac{X^2}4}=\sqrt{\frac34X^2+\frac32X-\frac94}=\frac12\sqrt{3X^2+6X-9}[/math]
Площадь трапеции:
[math]S=\frac{BC+AD}2CH=\frac{3+X}2\cdot\frac12\sqrt{3X^2+6X-9}=96[/math]
Получаем уравнение:
[math]\frac{3+X}4\sqrt{3X^2+6X-9}=96[/math]
[math]\sqrt{3X^2+6X-9}=\frac{384}{3+X}[/math]
Возведем обе части уравнения в квадрат, так как они обе положительные:
[math]\left(\sqrt{3X^2+6X-9}\right)^2=\left(\frac{384}{3+X}\right)^2[/math]
[math]3X^2+6X-9=\frac{147556}{9+6X+X^2}[/math]
[math]\left(3X^2+6X-9\right)\left(X^2+6X+9\right)=147556[/math]
[math]3X^4+24X^3+54X^2-147537=0[/math]
X4+8X3+18X2-49179=0
Корни данного уравнения находятся среди множителей числа 49179=13•13•9•97
Разделим многочлен (X4+8X3+18X2-49179) на (X-13)
[math]\frac{X^4+8X^3+18X^2-49179}{X-13}=X^3+21X^2+291X+3783[/math]
Значит X=13 один из корней уравнения X4+8X3+18X2-49179=0
Решения уравнения X3+21X2+291X+3783=0 являются отрицательными или комплексными числами, которые условию задачи не удовлетворяют.
AD=CD=AB=Х=13
P=AD+CD+AB+BC=13+13+13+3=42
Ответ: 42
Ответ:
Если диагональ трапеции делит её тупой угол пополам. то ∠ACB=∠ACD.
∠ABC=∠DAC - как накрест лежащие. Значит ∠ACB=∠ACD=∠DAC, следовательно △DAC - равнобедренный → AD=CD=AB=Х так как трапеция равнобедренная.
DH=(BC-AD)/2=(3-Х)/2
По теореме Пифагора в треугольнике △DCH:
CH2=CD2-DH2
[math]CH=\sqrt{X^2-\left(\frac{3-X}2\right)^2}=\sqrt{X^2-\frac94+\frac{3X}2-\frac{X^2}4}=\sqrt{\frac34X^2+\frac32X-\frac94}=\frac12\sqrt{3X^2+6X-9}[/math]
Площадь трапеции:
[math]S=\frac{BC+AD}2CH=\frac{3+X}2\cdot\frac12\sqrt{3X^2+6X-9}=96[/math]
Получаем уравнение:
[math]\frac{3+X}4\sqrt{3X^2+6X-9}=96[/math]
[math]\sqrt{3X^2+6X-9}=\frac{384}{3+X}[/math]
Возведем обе части уравнения в квадрат, так как они обе положительные:
[math]\left(\sqrt{3X^2+6X-9}\right)^2=\left(\frac{384}{3+X}\right)^2[/math]
[math]3X^2+6X-9=\frac{147556}{9+6X+X^2}[/math]
[math]\left(3X^2+6X-9\right)\left(X^2+6X+9\right)=147556[/math]
[math]3X^4+24X^3+54X^2-147537=0[/math]
X4+8X3+18X2-49179=0
Корни данного уравнения находятся среди множителей числа 49179=13•13•9•97
Разделим многочлен (X4+8X3+18X2-49179) на (X-13)
[math]\frac{X^4+8X^3+18X^2-49179}{X-13}=X^3+21X^2+291X+3783[/math]
Значит X=13 один из корней уравнения X4+8X3+18X2-49179=0
Решения уравнения X3+21X2+291X+3783=0 являются отрицательными или комплексными числами, которые условию задачи не удовлетворяют.
AD=CD=AB=Х=13
P=AD+CD+AB+BC=13+13+13+3=42
Ответ: 42
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.