Задание № 26493
В равностороннем треугольнике АВС из вершин А и В проведена окружность с центром в точке О, проходящая через точку пересечения медиан треугольника АВС и касающаяся его стороны ВС в её середине D. Из точки А проведена прямая, касающаяся этой окружности в точке Е так, что градусная мера угла ВАЕ меньше 30°. Найдите отношение площадей треугольника АВЕ и четырехугольника ВЕОD.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
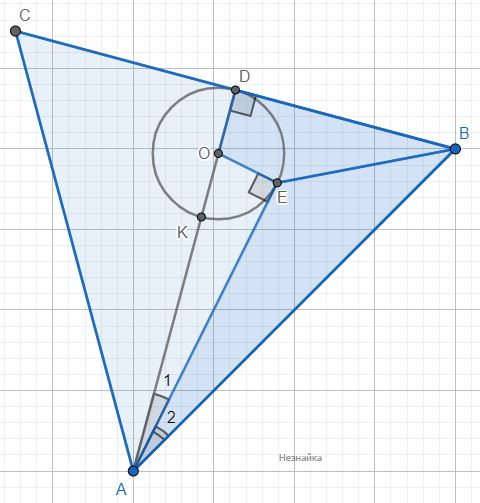Конечно же через вершины А и В, и еще через точку пересечения медиан, и еще через середину ВС провести окружность весьма проблематично, чтобы потом еще и была касательная, градусной меры менее 30°. Значит проводим окружность только через точку К пересечения медиан, касающуюся середины ВС. Дополнительно проведем отрезок AD - являющийся в правильном треугольнике и высотой, и медианой, и биссектрисой, так что окружность касается середины ВС в точке D и центр окружности О лежит на AD. Касательная АЕ образует угол ∠BAE<∠BAD=1/2∠BAC=1/2•60°=30°.
AB=BC=AC=a
OD=OE=OK=R
Медиана правильного треугольника: [math]AD=\frac{\sqrt3}2a[/math]
Медианы в точке пересечения делятся в отношении 2:1, считая от вершины:
[math]AK=\frac23AD=\frac{\sqrt3}3a[/math]
[math]KD=\frac13AD=\frac{\sqrt3}6a[/math]
[math]OK=OD=\frac12KD=\frac{\sqrt3}{12}a=OE=R[/math]
[math]AO=AK+OK=\frac{\sqrt3}3a+\frac{\sqrt3}{12}a=\frac{5\sqrt3}{12}a[/math]
По теореме Пифагора в △AEO:
[math]AE=\sqrt{AO^2-OE^2}=\sqrt{\left(\frac{5\sqrt3}{12}\right)^2-\left(\frac{\sqrt3}{12}\right)^2}=\frac{\sqrt2}2a[/math]
[math]sin\angle1=\frac{OE}{AO}=\frac{\frac{\sqrt3}{12}a}{\frac{5\sqrt3}{12}a}=\frac15[/math]
[math]cos\angle1=\frac{AE}{AO}=\frac{\frac{\sqrt2}2a}{\frac{5\sqrt3}{12}a}=\frac{2\sqrt6}5[/math]
[math]\angle1=arcsin\frac15=arccos\frac{2\sqrt6}5[/math]
[math]\angle2=30^\circ-\angle1[/math]
[math]sin\angle2=sin(30^\circ-\angle1)=sin30^\circ cos\angle1-cos30^\circ sin\angle1=\frac12\cdot\frac{2\sqrt6}5-\frac{\sqrt3}2\cdot\frac15=\frac{\sqrt6}5-\frac{\sqrt3}{10}[/math]
[math]S_{\bigtriangleup ABE}=\frac12AE\cdot AB\cdot sin\angle2=\frac12\cdot\frac{\sqrt2}2a\cdot a\cdot\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)=\frac{\sqrt2}4\cdot\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)a^2=[/math]
[math]=\frac{\sqrt2\left(2\sqrt6-\sqrt3\right)}{4\cdot10}a^2=\frac{\sqrt6(2\sqrt2-1)}{40}a^2[/math]
[math]S_{BEOD}=S_{\bigtriangleup ABD}-S_{\bigtriangleup ABE}-S_{\bigtriangleup AEO}[/math]
[math]S_{\bigtriangleup ABD}=\frac12AD\cdot BD=\frac12\cdot\frac{\sqrt3}2a\cdot\frac12a=\frac{\sqrt3}8a^2[/math]
[math]S_{\bigtriangleup AEO}=\frac12AE\cdot OE=\frac12\cdot\frac{\sqrt2}2a\cdot\frac{\sqrt3}{12}a=\frac{\sqrt6}{48}a^2[/math]
[math]S_{BEOD}=\frac{\sqrt3}8a^2-\frac{\sqrt2}4\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)a^2-\frac{\sqrt6}{48}a^2=[/math]
[math]=\frac{\sqrt3}8a^2-\frac{\sqrt3}{10}a^2+\frac{\sqrt6}{40}a^2-\frac{\sqrt6}{48}a^2=\frac{30\sqrt3-24\sqrt3+6\sqrt6-5\sqrt6}{240}a^2=\frac{6\sqrt3+\sqrt6}{240}a^2=\frac{\sqrt3\left(6+\sqrt2\right)}{240}a^2[/math]
[math]\frac{S_{\bigtriangleup ABE}}{S_{BEOD}}=\frac{\sqrt6\left(2\sqrt2-1\right)/40}{\sqrt3\left(6+\sqrt2\right)/240}=\frac{6\sqrt2\left(2\sqrt2-1\right)}{6+\sqrt2}=\frac{6\sqrt2\left(2\sqrt2-1\right)\left(6-\sqrt2\right)}{36-2}=\frac{3\sqrt2\left(12\sqrt2-4-6+\sqrt2\right)}{17}=\frac{3\sqrt2\left(13\sqrt2-10\right)}{17}=\frac{6\left(13-5\sqrt2\right)}{17}[/math]
Ответ: 6(13-5√2)/17
Ответ:
Конечно же через вершины А и В, и еще через точку пересечения медиан, и еще через середину ВС провести окружность весьма проблематично, чтобы потом еще и была касательная, градусной меры менее 30°. Значит проводим окружность только через точку К пересечения медиан, касающуюся середины ВС. Дополнительно проведем отрезок AD - являющийся в правильном треугольнике и высотой, и медианой, и биссектрисой, так что окружность касается середины ВС в точке D и центр окружности О лежит на AD. Касательная АЕ образует угол ∠BAE<∠BAD=1/2∠BAC=1/2•60°=30°.
AB=BC=AC=a
OD=OE=OK=R
Медиана правильного треугольника: [math]AD=\frac{\sqrt3}2a[/math]
Медианы в точке пересечения делятся в отношении 2:1, считая от вершины:
[math]AK=\frac23AD=\frac{\sqrt3}3a[/math]
[math]KD=\frac13AD=\frac{\sqrt3}6a[/math]
[math]OK=OD=\frac12KD=\frac{\sqrt3}{12}a=OE=R[/math]
[math]AO=AK+OK=\frac{\sqrt3}3a+\frac{\sqrt3}{12}a=\frac{5\sqrt3}{12}a[/math]
По теореме Пифагора в △AEO:
[math]AE=\sqrt{AO^2-OE^2}=\sqrt{\left(\frac{5\sqrt3}{12}\right)^2-\left(\frac{\sqrt3}{12}\right)^2}=\frac{\sqrt2}2a[/math]
[math]sin\angle1=\frac{OE}{AO}=\frac{\frac{\sqrt3}{12}a}{\frac{5\sqrt3}{12}a}=\frac15[/math]
[math]cos\angle1=\frac{AE}{AO}=\frac{\frac{\sqrt2}2a}{\frac{5\sqrt3}{12}a}=\frac{2\sqrt6}5[/math]
[math]\angle1=arcsin\frac15=arccos\frac{2\sqrt6}5[/math]
[math]\angle2=30^\circ-\angle1[/math]
[math]sin\angle2=sin(30^\circ-\angle1)=sin30^\circ cos\angle1-cos30^\circ sin\angle1=\frac12\cdot\frac{2\sqrt6}5-\frac{\sqrt3}2\cdot\frac15=\frac{\sqrt6}5-\frac{\sqrt3}{10}[/math]
[math]S_{\bigtriangleup ABE}=\frac12AE\cdot AB\cdot sin\angle2=\frac12\cdot\frac{\sqrt2}2a\cdot a\cdot\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)=\frac{\sqrt2}4\cdot\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)a^2=[/math]
[math]=\frac{\sqrt2\left(2\sqrt6-\sqrt3\right)}{4\cdot10}a^2=\frac{\sqrt6(2\sqrt2-1)}{40}a^2[/math]
[math]S_{BEOD}=S_{\bigtriangleup ABD}-S_{\bigtriangleup ABE}-S_{\bigtriangleup AEO}[/math]
[math]S_{\bigtriangleup ABD}=\frac12AD\cdot BD=\frac12\cdot\frac{\sqrt3}2a\cdot\frac12a=\frac{\sqrt3}8a^2[/math]
[math]S_{\bigtriangleup AEO}=\frac12AE\cdot OE=\frac12\cdot\frac{\sqrt2}2a\cdot\frac{\sqrt3}{12}a=\frac{\sqrt6}{48}a^2[/math]
[math]S_{BEOD}=\frac{\sqrt3}8a^2-\frac{\sqrt2}4\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)a^2-\frac{\sqrt6}{48}a^2=[/math]
[math]=\frac{\sqrt3}8a^2-\frac{\sqrt3}{10}a^2+\frac{\sqrt6}{40}a^2-\frac{\sqrt6}{48}a^2=\frac{30\sqrt3-24\sqrt3+6\sqrt6-5\sqrt6}{240}a^2=\frac{6\sqrt3+\sqrt6}{240}a^2=\frac{\sqrt3\left(6+\sqrt2\right)}{240}a^2[/math]
[math]\frac{S_{\bigtriangleup ABE}}{S_{BEOD}}=\frac{\sqrt6\left(2\sqrt2-1\right)/40}{\sqrt3\left(6+\sqrt2\right)/240}=\frac{6\sqrt2\left(2\sqrt2-1\right)}{6+\sqrt2}=\frac{6\sqrt2\left(2\sqrt2-1\right)\left(6-\sqrt2\right)}{36-2}=\frac{3\sqrt2\left(12\sqrt2-4-6+\sqrt2\right)}{17}=\frac{3\sqrt2\left(13\sqrt2-10\right)}{17}=\frac{6\left(13-5\sqrt2\right)}{17}[/math]
Ответ: 6(13-5√2)/17
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.