Вариант 5
Часть 1.
Ответами к заданиям 1–20 являются число или последовательность цифр, которые следует записать в поле соответствующего задания. Если ответом является последовательность цифр, то запишите её без пробелов, запятых и других дополнительных символов.
Прочитайте внимательно текст и выполните задания 1–5
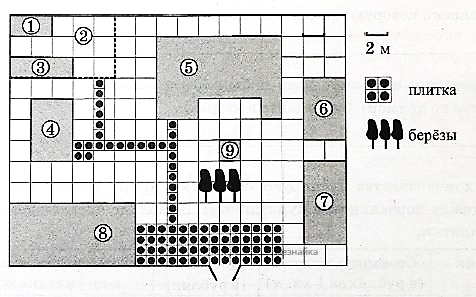
На плане изображено домохозяйство, находящееся по адресу: с. Малые Всегодичи, д. 26. Сторона каждой клетки на плане равна 2 м. Участок имеет форму прямоугольника. Выезд и въезд осуществляются через единственные ворота. При входе на участок справа от ворот находится коровник, а слева — курятник. Площадь, занятая курятником, равна 72 кв. м. Рядом с курятником расположен пруд площадью 24 кв. м. Жилой дом расположен в глубине территории. Перед домом имеется фонтан, а между фонтаном и воротами — небольшая берёзовая рощица. Между жилым домом и коровником построена баня. За домом находится огород (его границы отмечены на плане пунктирной линией), на котором есть теплица, а также (в самом углу и огорода, и всего домохозяйства) — компостная яма.
Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м х 1 м. Между коровником и курятником имеется площадка площадью 56 кв. м, вымощенная такой же плиткой.
Сопоставьте объекты, указанные в таблице, с цифрами, которыми эти объекты обозначены на плане. Заполните таблицу, а в бланк ответов перенесите последовательность из пяти цифр.
| Объекты | пруд | теплица | жилой дом | огород | курятник |
| Цифры |
Тротуарная плитка продаётся в упаковках по 7 штук. Сколько упаковок понадобилось купить владельцам домохозяйства для того, чтобы выложить все дорожки и площадку между коровником и курятником?
Найдите площадь, которую занимает коровник. Ответ дайте в квадратных метрах.
Найдите расстояние от бани до коровника (расстояние между двумя ближайшими точками объектов по прямой). Ответ дайте в метрах.
Владельцы домохозяйства планируют обновить всю тротуарную плитку (и дорожки, и площадку между коровником и курятником). В таблице представлены условия трёх поставщиков плитки.
| Поставщик | Стоимость плитки (в руб. за 1 кв.м.) | Доставка (в руб.) | Работы по демонтажу старой плитки и по укладке новой (в руб.) |
| 1 | 200 | 5600 | 4100 |
| 2 | 200 | 5000 | 4500 |
| 3 | 200 | 3000 | 7000 |
Найдите значение выражения
[math]\frac{2,8\cdot8,1}{6,3}[/math]
Сравните числа [math]\sqrt{15}+1[/math] и [math]3+\sqrt7[/math]
1) [math]\sqrt{15}+1<3+\sqrt7[/math]
2) [math]\sqrt{15}+1>3+\sqrt7[/math]
3) [math]\sqrt{15}+1=3+\sqrt7[/math]
4) нельзя оценить
Укажите выражение, тождественно равное дроби
[math]\frac{2^{2m}}{256}[/math]
1) [math]2^{2m-10}[/math]
2) [math]2^{8-2m}[/math]
3) [math]2^{2m-8}[/math]
4) [math]2^{16m}[/math]
Решите уравнение [math]\frac{3x+5}4=\frac x2[/math]
На новый год было закуплено 3 килограмма конфет «Мишка на севере», 1 килограмм конфет «Красная шапочка» и 1 килограмм конфет «Маска». Все конфеты одинаковы по плотности, и каждый килограмм содержит одинаковое количество конфет. Какова вероятность, что случайно взятая из мешка конфета окажется конфетой «Красная шапочка»?
На рисунке изображён график квадратичной функции [math]y=ax^{2}+bx+c[/math]
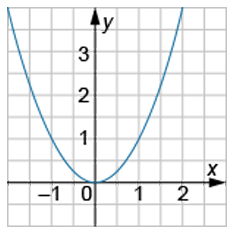
Определите, какому значению коэффициента a соответствует график?
1) —1
2) 0,5
3) 1
4) 2
Дана арифметическая прогрессия an : —5, —1, 3, ... . Найдите сумму первых 12-ти ее членов.
Упростите выражение [math]\frac{9x^2-6x+1}{7x^2}:\frac{3x-1}{14x}[/math] и найдите его значение при x = 2.
Ускорение тела при равноускоренном прямолинейном движении можно рассчитать по формуле [math]a=\frac{v-v_0}t[/math], где а — ускорение (км/ч2), v — приобретенная скорость (км/ч), v0 — начальная скорость (км/ч) и t — время равноускоренного движения (ч). С помощью формулы определите начальную скорость тела (в км/ч), если ускорение равно 3 км/ч2, приобретенная скорость 90 км/ч, а время равноускоренного движения 4 часа.
Решите неравенство [math]-x^2-4x+5<0[/math]
1) [math]x\in(-\infty;-5)\cup(1;+\infty)[/math]
2) [math]x\in(-5;1)[/math]
3) [math]x\in\lbrack-5;1\rbrack[/math]
4) [math]x\in\lbrack1;+\infty)[/math]
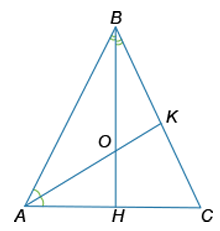
В равнобедренном треугольнике ABC с боковыми сторонами AB и BC проведены биссектрисы BH и AK, которые пересекаются в точке O. Найдите угол AOH, если угол C равен [math]50^\circ[/math].
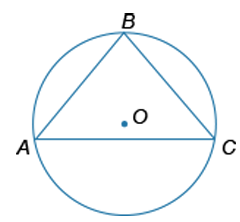
В окружность с центром в точке O вписан равнобедренный треугольник ABC с основанием AC. Дуга ACB равна [math]260^\circ[/math]. Найдите угол ABC
Найдите площадь параллелограмма (в см2), стороны которого равны 7 см и 4 см, а угол между ними равен [math]30^\circ[/math].
Найдите площадь фигуры, изображённой на рисунке, если сторона клетки равна 1 см. Ответ запишите в см2.
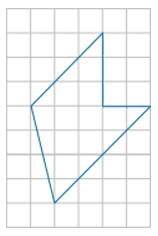
Какое из приведённых утверждений верно? Выберите 2 варианта из списка.
1) Катет, лежащий против угла в [math]30^\circ[/math], равен 1/3 гипотенузы.
2) Площадь трапеции равна произведению её оснований на высоту.
3) Сумма смежных углов равна [math]180^\circ[/math]
4) Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Часть 2.
При выполнении заданий 21–26 используйте тетрадь. Сначала укажите номер задания, а затем запишите его решение и ответ. Пишите чётко и разборчиво.
Решите неравенство [math]\frac x{1-x}\leq x-6[/math]
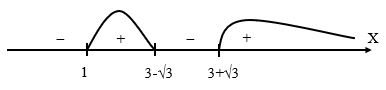 Ответ: (1;3 -√3], [3+√3; ∞)
Ответ: (1;3 -√3], [3+√3; ∞)Теплоход затратил 5 часов на путь вниз по течению реки от пункта A до пункта B. На обратный путь против течения он затратил 8 часов 20 минут. Найти скорость теплохода, если путь от A до B равен 100 километрам.
Постройте график функции [math]y=\frac{\left(\sqrt{x^2-5x+6}\right)^2}{x-3}[/math] и найдите все значения а при которых прямая у = a не имеет с графиком ни одной общей точки.
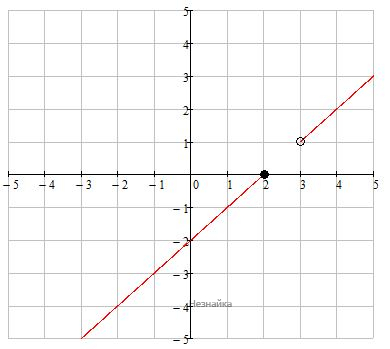 Прямая y = a параллельна оси ОХ и не имеет с графиком ни одной общей точки при aє(0;1] Ответ: (0;1]
Прямая y = a параллельна оси ОХ и не имеет с графиком ни одной общей точки при aє(0;1] Ответ: (0;1]В равнобедренной трапеции основания равны 12 см и 20 см, а диагонали взаимно перпендикулярны. Найдите площадь трапеции.
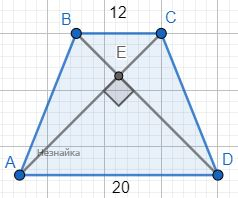 В равнобедренной трапеции диагонали равны. Так как они перпендикулярны, то получаем два равнобедренных прямоугольных треугольника △EBC и △EAD, у которых известны гипотенузы. Катеты △EBC и △EAD в √2 раза меньше гипотенуз. Получаем BE=CE=6√2 AE=DE=10√2 AC=BD=16√2 [math]S=\frac{AC\cdot BD}2sin(\angle AED)[/math] [math]S=\frac{16\sqrt2\cdot16\sqrt2}2sin(90^\circ)=256[/math] Ответ: 256
В равнобедренной трапеции диагонали равны. Так как они перпендикулярны, то получаем два равнобедренных прямоугольных треугольника △EBC и △EAD, у которых известны гипотенузы. Катеты △EBC и △EAD в √2 раза меньше гипотенуз. Получаем BE=CE=6√2 AE=DE=10√2 AC=BD=16√2 [math]S=\frac{AC\cdot BD}2sin(\angle AED)[/math] [math]S=\frac{16\sqrt2\cdot16\sqrt2}2sin(90^\circ)=256[/math] Ответ: 256На высоте AD треугольника ABC взята точка N. Докажите, что [math]AB^2-AC^2=BN^2-CN^2[/math]
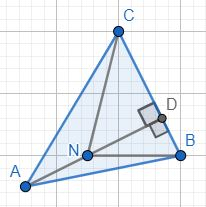 По теореме Пифагора в △NDB и △NDC: CN2=CD2+ND2 BN2=BD2+ND2 BN2-CN2=BD2+ND2-(CD2+ND2)=BD2-CD2 В △ADB и △ADC: AC2=CD2+AD2 AB2=BD2+AD2 AB2-AC2=BD2-CD2 Значит: BN2-CN2=BD2-CD2=AB2-AC2
По теореме Пифагора в △NDB и △NDC: CN2=CD2+ND2 BN2=BD2+ND2 BN2-CN2=BD2+ND2-(CD2+ND2)=BD2-CD2 В △ADB и △ADC: AC2=CD2+AD2 AB2=BD2+AD2 AB2-AC2=BD2-CD2 Значит: BN2-CN2=BD2-CD2=AB2-AC2В равностороннем треугольнике АВС из вершин А и В проведена окружность с центром в точке О, проходящая через точку пересечения медиан треугольника АВС и касающаяся его стороны ВС в её середине D. Из точки А проведена прямая, касающаяся этой окружности в точке Е так, что градусная мера угла ВАЕ меньше 30°. Найдите отношение площадей треугольника АВЕ и четырехугольника ВЕОD.
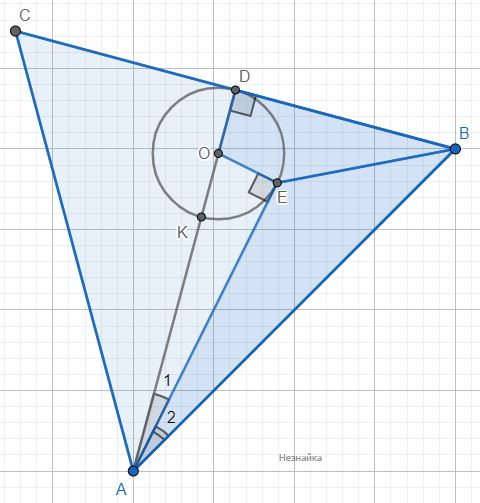 Конечно же через вершины А и В, и еще через точку пересечения медиан, и еще через середину ВС провести окружность весьма проблематично, чтобы потом еще и была касательная, градусной меры менее 30°. Значит проводим окружность только через точку К пересечения медиан, касающуюся середины ВС. Дополнительно проведем отрезок AD - являющийся в правильном треугольнике и высотой, и медианой, и биссектрисой, так что окружность касается середины ВС в точке D и центр окружности О лежит на AD. Касательная АЕ образует угол ∠BAE<∠BAD=1/2∠BAC=1/2•60°=30°. AB=BC=AC=a OD=OE=OK=R Медиана правильного треугольника: [math]AD=\frac{\sqrt3}2a[/math] Медианы в точке пересечения делятся в отношении 2:1, считая от вершины: [math]AK=\frac23AD=\frac{\sqrt3}3a[/math] [math]KD=\frac13AD=\frac{\sqrt3}6a[/math] [math]OK=OD=\frac12KD=\frac{\sqrt3}{12}a=OE=R[/math] [math]AO=AK+OK=\frac{\sqrt3}3a+\frac{\sqrt3}{12}a=\frac{5\sqrt3}{12}a[/math] По теореме Пифагора в △AEO: [math]AE=\sqrt{AO^2-OE^2}=\sqrt{\left(\frac{5\sqrt3}{12}\right)^2-\left(\frac{\sqrt3}{12}\right)^2}=\frac{\sqrt2}2a[/math] [math]sin\angle1=\frac{OE}{AO}=\frac{\frac{\sqrt3}{12}a}{\frac{5\sqrt3}{12}a}=\frac15[/math] [math]cos\angle1=\frac{AE}{AO}=\frac{\frac{\sqrt2}2a}{\frac{5\sqrt3}{12}a}=\frac{2\sqrt6}5[/math] [math]\angle1=arcsin\frac15=arccos\frac{2\sqrt6}5[/math] [math]\angle2=30^\circ-\angle1[/math] [math]sin\angle2=sin(30^\circ-\angle1)=sin30^\circ cos\angle1-cos30^\circ sin\angle1=\frac12\cdot\frac{2\sqrt6}5-\frac{\sqrt3}2\cdot\frac15=\frac{\sqrt6}5-\frac{\sqrt3}{10}[/math] [math]S_{\bigtriangleup ABE}=\frac12AE\cdot AB\cdot sin\angle2=\frac12\cdot\frac{\sqrt2}2a\cdot a\cdot\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)=\frac{\sqrt2}4\cdot\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)a^2=[/math] [math]=\frac{\sqrt2\left(2\sqrt6-\sqrt3\right)}{4\cdot10}a^2=\frac{\sqrt6(2\sqrt2-1)}{40}a^2[/math] [math]S_{BEOD}=S_{\bigtriangleup ABD}-S_{\bigtriangleup ABE}-S_{\bigtriangleup AEO}[/math] [math]S_{\bigtriangleup ABD}=\frac12AD\cdot BD=\frac12\cdot\frac{\sqrt3}2a\cdot\frac12a=\frac{\sqrt3}8a^2[/math] [math]S_{\bigtriangleup AEO}=\frac12AE\cdot OE=\frac12\cdot\frac{\sqrt2}2a\cdot\frac{\sqrt3}{12}a=\frac{\sqrt6}{48}a^2[/math] [math]S_{BEOD}=\frac{\sqrt3}8a^2-\frac{\sqrt2}4\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)a^2-\frac{\sqrt6}{48}a^2=[/math] [math]=\frac{\sqrt3}8a^2-\frac{\sqrt3}{10}a^2+\frac{\sqrt6}{40}a^2-\frac{\sqrt6}{48}a^2=\frac{30\sqrt3-24\sqrt3+6\sqrt6-5\sqrt6}{240}a^2=\frac{6\sqrt3+\sqrt6}{240}a^2=\frac{\sqrt3\left(6+\sqrt2\right)}{240}a^2[/math] [math]\frac{S_{\bigtriangleup ABE}}{S_{BEOD}}=\frac{\sqrt6\left(2\sqrt2-1\right)/40}{\sqrt3\left(6+\sqrt2\right)/240}=\frac{6\sqrt2\left(2\sqrt2-1\right)}{6+\sqrt2}=\frac{6\sqrt2\left(2\sqrt2-1\right)\left(6-\sqrt2\right)}{36-2}=\frac{3\sqrt2\left(12\sqrt2-4-6+\sqrt2\right)}{17}=\frac{3\sqrt2\left(13\sqrt2-10\right)}{17}=\frac{6\left(13-5\sqrt2\right)}{17}[/math] Ответ: 6(13-5√2)/17
Конечно же через вершины А и В, и еще через точку пересечения медиан, и еще через середину ВС провести окружность весьма проблематично, чтобы потом еще и была касательная, градусной меры менее 30°. Значит проводим окружность только через точку К пересечения медиан, касающуюся середины ВС. Дополнительно проведем отрезок AD - являющийся в правильном треугольнике и высотой, и медианой, и биссектрисой, так что окружность касается середины ВС в точке D и центр окружности О лежит на AD. Касательная АЕ образует угол ∠BAE<∠BAD=1/2∠BAC=1/2•60°=30°. AB=BC=AC=a OD=OE=OK=R Медиана правильного треугольника: [math]AD=\frac{\sqrt3}2a[/math] Медианы в точке пересечения делятся в отношении 2:1, считая от вершины: [math]AK=\frac23AD=\frac{\sqrt3}3a[/math] [math]KD=\frac13AD=\frac{\sqrt3}6a[/math] [math]OK=OD=\frac12KD=\frac{\sqrt3}{12}a=OE=R[/math] [math]AO=AK+OK=\frac{\sqrt3}3a+\frac{\sqrt3}{12}a=\frac{5\sqrt3}{12}a[/math] По теореме Пифагора в △AEO: [math]AE=\sqrt{AO^2-OE^2}=\sqrt{\left(\frac{5\sqrt3}{12}\right)^2-\left(\frac{\sqrt3}{12}\right)^2}=\frac{\sqrt2}2a[/math] [math]sin\angle1=\frac{OE}{AO}=\frac{\frac{\sqrt3}{12}a}{\frac{5\sqrt3}{12}a}=\frac15[/math] [math]cos\angle1=\frac{AE}{AO}=\frac{\frac{\sqrt2}2a}{\frac{5\sqrt3}{12}a}=\frac{2\sqrt6}5[/math] [math]\angle1=arcsin\frac15=arccos\frac{2\sqrt6}5[/math] [math]\angle2=30^\circ-\angle1[/math] [math]sin\angle2=sin(30^\circ-\angle1)=sin30^\circ cos\angle1-cos30^\circ sin\angle1=\frac12\cdot\frac{2\sqrt6}5-\frac{\sqrt3}2\cdot\frac15=\frac{\sqrt6}5-\frac{\sqrt3}{10}[/math] [math]S_{\bigtriangleup ABE}=\frac12AE\cdot AB\cdot sin\angle2=\frac12\cdot\frac{\sqrt2}2a\cdot a\cdot\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)=\frac{\sqrt2}4\cdot\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)a^2=[/math] [math]=\frac{\sqrt2\left(2\sqrt6-\sqrt3\right)}{4\cdot10}a^2=\frac{\sqrt6(2\sqrt2-1)}{40}a^2[/math] [math]S_{BEOD}=S_{\bigtriangleup ABD}-S_{\bigtriangleup ABE}-S_{\bigtriangleup AEO}[/math] [math]S_{\bigtriangleup ABD}=\frac12AD\cdot BD=\frac12\cdot\frac{\sqrt3}2a\cdot\frac12a=\frac{\sqrt3}8a^2[/math] [math]S_{\bigtriangleup AEO}=\frac12AE\cdot OE=\frac12\cdot\frac{\sqrt2}2a\cdot\frac{\sqrt3}{12}a=\frac{\sqrt6}{48}a^2[/math] [math]S_{BEOD}=\frac{\sqrt3}8a^2-\frac{\sqrt2}4\left(\frac{\sqrt6}5-\frac{\sqrt3}{10}\right)a^2-\frac{\sqrt6}{48}a^2=[/math] [math]=\frac{\sqrt3}8a^2-\frac{\sqrt3}{10}a^2+\frac{\sqrt6}{40}a^2-\frac{\sqrt6}{48}a^2=\frac{30\sqrt3-24\sqrt3+6\sqrt6-5\sqrt6}{240}a^2=\frac{6\sqrt3+\sqrt6}{240}a^2=\frac{\sqrt3\left(6+\sqrt2\right)}{240}a^2[/math] [math]\frac{S_{\bigtriangleup ABE}}{S_{BEOD}}=\frac{\sqrt6\left(2\sqrt2-1\right)/40}{\sqrt3\left(6+\sqrt2\right)/240}=\frac{6\sqrt2\left(2\sqrt2-1\right)}{6+\sqrt2}=\frac{6\sqrt2\left(2\sqrt2-1\right)\left(6-\sqrt2\right)}{36-2}=\frac{3\sqrt2\left(12\sqrt2-4-6+\sqrt2\right)}{17}=\frac{3\sqrt2\left(13\sqrt2-10\right)}{17}=\frac{6\left(13-5\sqrt2\right)}{17}[/math] Ответ: 6(13-5√2)/17 | № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||