Задание № 26476
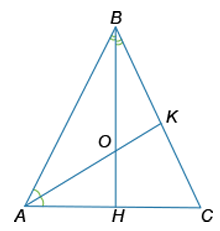
В равнобедренном треугольнике ABC с боковыми сторонами AB и BC проведены биссектрисы BH и AK, которые пересекаются в точке O. Найдите угол AOH, если угол C равен [math]50^\circ[/math].
Решать другие задания по теме: Треугольники, четырёхугольники, многоугольники и их элементы
Показать ответ
Комментарий:
В равнобедренном треугольнике углы при основании равны между собой: ∠С=∠А=50°. Так как АК биссектриса, то ∠ОАН=∠А/2=25° Биссектриса BH, проведенная к основанию равнобедренного треугольника, является высотой, т.е. ∠ОНА=90°. Сумма углов в треугольнике АОН равна 180°: ∠AOH=180°-∠ОНА-∠ОАН=65° Ответ: 65
В равнобедренном треугольнике углы при основании равны между собой: ∠С=∠А=50°. Так как АК биссектриса, то ∠ОАН=∠А/2=25° Биссектриса BH, проведенная к основанию равнобедренного треугольника, является высотой, т.е. ∠ОНА=90°. Сумма углов в треугольнике АОН равна 180°: ∠AOH=180°-∠ОНА-∠ОАН=65° Ответ: 65
Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.