Задание № 26466
Докажите, что если в треугольнике два угла равны, то он равнобедренный.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
1 способ В треугольнике против бОльшего угла лежит бОльшая сторона. Следствие: против равных углов лежат равные стороны. Таким образом, если в треугольнике два угла равны, то лежащие напротив этих углов стороны тоже равны, а значит, треугольник — равнобедренный. 2 способ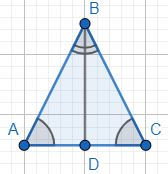
Проведем биссектрису BD, получим два треугольника у которых равны углы: ∠DBA=∠DBC, ∠DAB=∠DCB - значит равны и углы ∠BDA=∠BDC, так как сумма углов в треугольнике всегда 180°.
Треугольники △DBA=△DBC равны между собой по двум углам ∠DBA=∠DBC , ∠BDA=∠BDC и общей стороне BD
Так как треугольники равны, то их стороны тоже равны AB=BC - треугольник равнобедренный по определению.
Ответ:
1 способ В треугольнике против бОльшего угла лежит бОльшая сторона. Следствие: против равных углов лежат равные стороны. Таким образом, если в треугольнике два угла равны, то лежащие напротив этих углов стороны тоже равны, а значит, треугольник — равнобедренный. 2 способ
Проведем биссектрису BD, получим два треугольника у которых равны углы: ∠DBA=∠DBC, ∠DAB=∠DCB - значит равны и углы ∠BDA=∠BDC, так как сумма углов в треугольнике всегда 180°.
Треугольники △DBA=△DBC равны между собой по двум углам ∠DBA=∠DBC , ∠BDA=∠BDC и общей стороне BD
Так как треугольники равны, то их стороны тоже равны AB=BC - треугольник равнобедренный по определению.
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.