Задание № 26465
Основания трапеции равны 6 см и 18 см. Через точку пересечения диагоналей проведена прямая, параллельная основаниям, до пересечения с боковыми сторонами. Найдите длину отрезка этой прямой.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
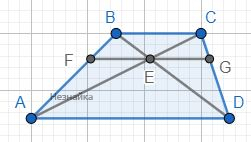 Треугольники △AED и △CEB подобны по двум углам: ∠AED=∠CEB, ∠CAD=ACB (накрест лежащие).
[math]\frac{EC}{AE}=\frac{BC}{AD}=\frac6{18}=\frac13[/math]
[math]AE=3EC[/math]
Треугольники △ACB и △AEF подобны, так как FG параллельно BC
[math]\frac{FE}{BC}=\frac{AE}{AC}=\frac{AE}{AE+EC}=\frac{3EC}{3EC+EC}=\frac34[/math]
[math]FE=\frac34BC=\frac34\cdot6=4,5[/math]
Треугольники △ACD и ECD подобны, так как FG параллельно BC
[math]\frac{EG}{AD}=\frac{EC}{AC}=\frac{EC}{AE+EC}=\frac{EC}{3EC+EC}=\frac14[/math]
[math]EG=\frac14AD=\frac14\cdot18=4,5[/math]
[math]FG=FE+EG=4,5+4,5=9[/math]
Ответ: 9
Ответ:
Треугольники △AED и △CEB подобны по двум углам: ∠AED=∠CEB, ∠CAD=ACB (накрест лежащие).
[math]\frac{EC}{AE}=\frac{BC}{AD}=\frac6{18}=\frac13[/math]
[math]AE=3EC[/math]
Треугольники △ACB и △AEF подобны, так как FG параллельно BC
[math]\frac{FE}{BC}=\frac{AE}{AC}=\frac{AE}{AE+EC}=\frac{3EC}{3EC+EC}=\frac34[/math]
[math]FE=\frac34BC=\frac34\cdot6=4,5[/math]
Треугольники △ACD и ECD подобны, так как FG параллельно BC
[math]\frac{EG}{AD}=\frac{EC}{AC}=\frac{EC}{AE+EC}=\frac{EC}{3EC+EC}=\frac14[/math]
[math]EG=\frac14AD=\frac14\cdot18=4,5[/math]
[math]FG=FE+EG=4,5+4,5=9[/math]
Ответ: 9
Ответ:
 Треугольники △AED и △CEB подобны по двум углам: ∠AED=∠CEB, ∠CAD=ACB (накрест лежащие).
[math]\frac{EC}{AE}=\frac{BC}{AD}=\frac6{18}=\frac13[/math]
[math]AE=3EC[/math]
Треугольники △ACB и △AEF подобны, так как FG параллельно BC
[math]\frac{FE}{BC}=\frac{AE}{AC}=\frac{AE}{AE+EC}=\frac{3EC}{3EC+EC}=\frac34[/math]
[math]FE=\frac34BC=\frac34\cdot6=4,5[/math]
Треугольники △ACD и ECD подобны, так как FG параллельно BC
[math]\frac{EG}{AD}=\frac{EC}{AC}=\frac{EC}{AE+EC}=\frac{EC}{3EC+EC}=\frac14[/math]
[math]EG=\frac14AD=\frac14\cdot18=4,5[/math]
[math]FG=FE+EG=4,5+4,5=9[/math]
Ответ: 9
Ответ:
Треугольники △AED и △CEB подобны по двум углам: ∠AED=∠CEB, ∠CAD=ACB (накрест лежащие).
[math]\frac{EC}{AE}=\frac{BC}{AD}=\frac6{18}=\frac13[/math]
[math]AE=3EC[/math]
Треугольники △ACB и △AEF подобны, так как FG параллельно BC
[math]\frac{FE}{BC}=\frac{AE}{AC}=\frac{AE}{AE+EC}=\frac{3EC}{3EC+EC}=\frac34[/math]
[math]FE=\frac34BC=\frac34\cdot6=4,5[/math]
Треугольники △ACD и ECD подобны, так как FG параллельно BC
[math]\frac{EG}{AD}=\frac{EC}{AC}=\frac{EC}{AE+EC}=\frac{EC}{3EC+EC}=\frac14[/math]
[math]EG=\frac14AD=\frac14\cdot18=4,5[/math]
[math]FG=FE+EG=4,5+4,5=9[/math]
Ответ: 9
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.