Задание № 26413
Через концы хорды, длина которой 30, проведены две касательные, до пересечения в точке А. Найдите расстояние от точки А до хорды, если радиус окружности равен 17.
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
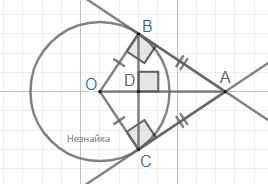 OB=OC=17 - радиусы, значит они перпендикулярны соответствующим касательным BA и CA. Прямоугольные треугольники ABO и ACO равны между собой по катету и общей гипотенузе, поэтому AB=AC, треугольник ABC - равнобедренный и AD - биссектриса ∠BAC. Таким образом, AD - еще и высота, и медиана равнобедренного треугольника, и искомое расстояние от точки А до хорды.
В прямоугольном △OBD : OB=17, BD=30/2=15. По теореме Пифагора OD=√(OB2-BD2)=8
По теореме о пропорциональных отрезках: BD2=OD•AD
AD=BD2/OD=152/8=28,125
Ответ: 28,125
Ответ:
OB=OC=17 - радиусы, значит они перпендикулярны соответствующим касательным BA и CA. Прямоугольные треугольники ABO и ACO равны между собой по катету и общей гипотенузе, поэтому AB=AC, треугольник ABC - равнобедренный и AD - биссектриса ∠BAC. Таким образом, AD - еще и высота, и медиана равнобедренного треугольника, и искомое расстояние от точки А до хорды.
В прямоугольном △OBD : OB=17, BD=30/2=15. По теореме Пифагора OD=√(OB2-BD2)=8
По теореме о пропорциональных отрезках: BD2=OD•AD
AD=BD2/OD=152/8=28,125
Ответ: 28,125
Ответ:
 OB=OC=17 - радиусы, значит они перпендикулярны соответствующим касательным BA и CA. Прямоугольные треугольники ABO и ACO равны между собой по катету и общей гипотенузе, поэтому AB=AC, треугольник ABC - равнобедренный и AD - биссектриса ∠BAC. Таким образом, AD - еще и высота, и медиана равнобедренного треугольника, и искомое расстояние от точки А до хорды.
В прямоугольном △OBD : OB=17, BD=30/2=15. По теореме Пифагора OD=√(OB2-BD2)=8
По теореме о пропорциональных отрезках: BD2=OD•AD
AD=BD2/OD=152/8=28,125
Ответ: 28,125
Ответ:
OB=OC=17 - радиусы, значит они перпендикулярны соответствующим касательным BA и CA. Прямоугольные треугольники ABO и ACO равны между собой по катету и общей гипотенузе, поэтому AB=AC, треугольник ABC - равнобедренный и AD - биссектриса ∠BAC. Таким образом, AD - еще и высота, и медиана равнобедренного треугольника, и искомое расстояние от точки А до хорды.
В прямоугольном △OBD : OB=17, BD=30/2=15. По теореме Пифагора OD=√(OB2-BD2)=8
По теореме о пропорциональных отрезках: BD2=OD•AD
AD=BD2/OD=152/8=28,125
Ответ: 28,125
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.