Условие данной задачи составлено некорректно

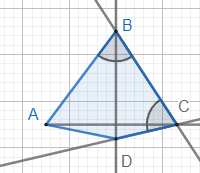
Здесь либо не хватает указания, что углы образованные диагоналями при вершинах В и С равны, либо чего то еще неведомого, но задуманного составителем заданий для ОГЭ. Так или иначе, надо решать это.

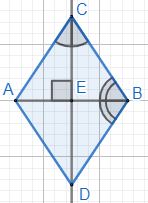
Прямоугольные треугольники ACE и BCE равны между собой по острому углу ∠ACE=∠BCE и общему катету CE. Тогда углы ∠CAE=∠CBE=∠DBE равны между собой.

Углы ∠CAE=∠DBE равны и являются накрест лежащими при прямых AC и BD и секущей AB, значит прямые AC и BD параллельны.