Задание № 26361
Высота, опущенная на гипотенузу прямоугольного треугольника, делит его на два треугольника, площади которых равны соответственно 6 и 54. Найдите гипотенузу треугольника
[topic]
Решать другие задания по теме: {topic-name}
[topic]
Показать ответ
Комментарий:
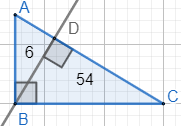 SABD=AD•BD/2=6
AD=12/BD
SBCD=DC•BD/2=54
DC=108/BD
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
[math]BD=\sqrt{AD\cdot DC}=\sqrt{\frac{12}{BD}\cdot\frac{108}{BD}}=\frac{36}{BD}[/math]
BD2=36
BD=6
SABC=AC•BD/2=6+54
AC=60•2/BD=20
Ответ: 20
Ответ:
SABD=AD•BD/2=6
AD=12/BD
SBCD=DC•BD/2=54
DC=108/BD
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
[math]BD=\sqrt{AD\cdot DC}=\sqrt{\frac{12}{BD}\cdot\frac{108}{BD}}=\frac{36}{BD}[/math]
BD2=36
BD=6
SABC=AC•BD/2=6+54
AC=60•2/BD=20
Ответ: 20
Ответ:
 SABD=AD•BD/2=6
AD=12/BD
SBCD=DC•BD/2=54
DC=108/BD
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
[math]BD=\sqrt{AD\cdot DC}=\sqrt{\frac{12}{BD}\cdot\frac{108}{BD}}=\frac{36}{BD}[/math]
BD2=36
BD=6
SABC=AC•BD/2=6+54
AC=60•2/BD=20
Ответ: 20
Ответ:
SABD=AD•BD/2=6
AD=12/BD
SBCD=DC•BD/2=54
DC=108/BD
Высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу.
[math]BD=\sqrt{AD\cdot DC}=\sqrt{\frac{12}{BD}\cdot\frac{108}{BD}}=\frac{36}{BD}[/math]
BD2=36
BD=6
SABC=AC•BD/2=6+54
AC=60•2/BD=20
Ответ: 20
Ответ: Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.