Решение:

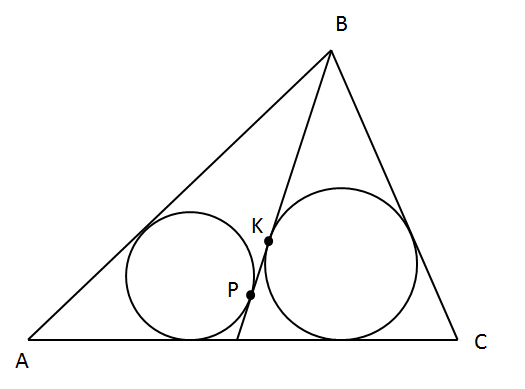
А)Найдем радиус вписанной окружности через следующую формулу: [math]S=pr[/math], где [math]p=\\frac P2[/math]

Отсюда [math]r=\\frac{2S}P[/math]

Радиус вписанной окружности в треугольник ABM: [math]r_{ABM}=\\frac{2S_{ABM}}{AB+BM+AM}[/math]

Радиус вписанной окружности в треугольник ABC: [math]r_{ABC}=\\frac{2S_{ABC}}{AB+BC+AC}[/math]

Пусть [math]r_{ABM}=\\frac12r_{ABC}[/math]. Тогда

[math]\\frac{2S_{ABM}}{AB+BM+AM}=\\frac{2S_{ABC}}{AB+BC+AC}[/math]

[math]S_{ABC}=2S_{ABM}[/math] , т.к. BM-медиана

Следовательно, знаменатели равны, т.е [math]BM+AM=BC+2AM[/math][math]BC+AM=BM[/math]

Б) Исходя из свойства о том,что прямые, выходящие из одной точки и касающиеся окружности, образуют два равных по величине отрезка, получим следующие выражения [math]MP=p_{ABM}-AB=\\frac{BM+AM}2-8.5=\\frac{BM+MC}2-8.5[/math]

[math]MК=p_{СBM}-BC=\\frac{BM+CM}2-3.5[/math]

Получим, что [math]PK=MK-MP=-3.5+8=5[/math]

Ответ: А) нет; Б) 5