Задание № 21811
В прямоугольном параллелепипеде ABCDA1B1C1D1 точка К лежит на ребре ВВ1 так, что КВ:КВ1=1:4. Плоскость α, проходящая через точки К и С1 параллельно прямой BD1, пересекает ребро АА1 в точке Р.
А) Докажите, что АР:А1Р=2:3.
Б) Найдите объем пирамиды, основанием которой является сечение параллелепипеда плоскостью α, а вершиной точка В1, если известно, что АВ=3, ВС=4, ВВ1=5.
Решение:
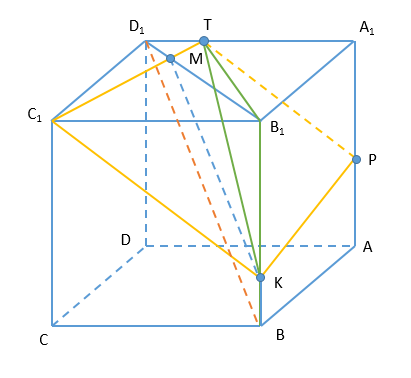
А) 1. Проведем [math]KM\vert\vert BD_1[/math], [math]M\in(BB_1D_1)[/math] , [math]M\in(A_1B_1C_1)[/math]
Проведем [math]CM\cap A_1D_1=T[/math]
[math](BB_1C)\vert\vert(ADD_1)\Rightarrow T\in AA_1[/math] [math]TP\vert\vert KC_1[/math]
Имеем, что [math](PTK)[/math]-плоскость, [math]PTC_1K[/math]-сечение параллелепипеда плоскостью [math]\alpha[/math]
2. [math]\bigtriangleup B_1MK[/math] и [math]\bigtriangleup B_1D_1B[/math] - подобны ([math]\angle B_1[/math]-j,общий, [math]KM\vert\vert BD_1\Rightarrow\angle B_1MK=\angle B_1D_1B[/math])[math]\Rightarrow[/math] [math]\frac{D_1M}{MB_1}=\frac{BK}{KB_1}=\frac14[/math]
[math]\bigtriangleup C_1MB_1\sim\bigtriangleup TMD_1[/math] (все углы попарно равны)[math]\Rightarrow[/math][math]\frac{D_1T}{B_1C_1}=\frac{D_1M}{MB_1}=\frac14[/math]
[math]\frac{A_1T}{B_1C_1}=\frac34[/math]
[math]\bigtriangleup PA_1T\sim\bigtriangleup KB_1C_1[/math] [math]\Rightarrow[/math] [math]\frac{A_1P}{B_1K}=\frac{A_1T}{B_1C_1}=\frac34[/math]
Получим, что [math]A_1P=\frac35BB_1[/math]. Тогда [math]AP=\frac25BB_1[/math]
[math]\frac{AP}{AP_1}=\frac23[/math], чтд
Б) [math](TB_1K)[/math] делит пирамиду [math]B_1TC_1KP[/math]на две пирамиды. Найдем их объем:
[math]V_{B_1TC_1K}=\frac13\cdot S_{B_1C_1K}\cdot С_1D_1=\frac13\cdot\frac12\cdot4\cdot4\cdot3=8[/math]
[math]V_{B_1TPK}=\frac13\cdot S_{B_1PK}\cdot A_1T=\frac13\cdot\frac12\cdot4\cdot3\cdot3=6[/math]
[math]V_{B_1TPKC_1}=8+6=14[/math]
Ответ: 14
Ответ:Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.