Задание № 21777
Найдите все а, при каждом из которых система уравнений
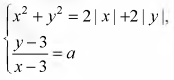
имеет ровно три различных решения.
Решение: преобразуем первое уравнение: [math](\left|x\right|-1)^2+(\left|y\right|-1)^2=2[/math]
Имеем окружность с радиусом [math]R=\sqrt2[/math] и центром О(1,1). Пример применим свойства модулей на графике и получим следующее:

Точка (0;0) тоже входит в график окружности. Чтобы получить гарантированно три решения, должна быть одна точка-фиксированная,т. е получим следующие варианты :

Уравнение прямой: [math]y=ax+(3-3a)[/math]
1 сл: y=0, x=2. Тогда а=3
2 сл: x=0, y=2. Тогда а= 1/3
3 сл: y=0, x=0. тогда а=1
4 и 5 сл: прямая касается одного сектора и пересекает второй в двух точках. Найдем уравнение касательной: [math]x^2-2x+y^2-2y=0[/math]
[math]a_4=-2;a_5=-2;a_6=0[/math]
Получаем уравнение касательной: [math](x_0+\frac{-2}2)x+(\frac{-2}2+y_0)y+(\frac{-2x_0-2y_0}2+0)=0[/math]
[math](x_0+-1)x+(-1+y_0)y+(-x_0-y_0)=0[/math]
Все прямые проходят через точку (3;3), то есть имеем уравнение [math]3(x_0+-1)+3(-1+y_0)+(-x_0-y_0)=0[/math] и исходное уравнение [math]-y_0+ax_0+(-3a+3)[/math]
Решим систему из этих двух уравнение и получим следующие значения:[math]x_0=\frac{3a}{1+a}[/math] [math]y_0=3-\frac{3a}{1+a}[/math]
Подставим в уравнение окружности первого сектора и получим квадратное уравнение: [math]3a^2-12a+3=0[/math]
Решение уравнения: [math]a_{1,2}=2\pm\sqrt3[/math]
Ответ: [math]2-\sqrt3;\;\frac13;\;1;\;3;\;2+\sqrt3[/math]
Ответ:Нашли ошибку в задании? Выделите фрагмент и нажмите Ctrl + Enter.