Решение:

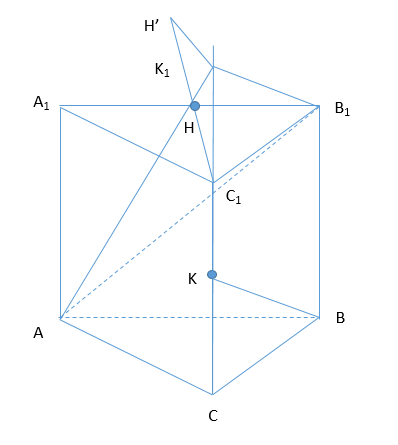
Все ребра равны, правильная призма, [math]C_1K=CK[/math]

А) Доказать, что [math]AB_1\perp KB[/math]

Совершим параллельный перенос прямой КВ так, чтобы она проходила через точку [math]B_1[/math], пересекает [math]С_1С[/math] в т. [math]К_1[/math]

[math]\bigtriangleup СВК=\bigtriangleup С_1В_1К_1[/math] (по катет и острому углу):

[math]С_1В_1=СВ[/math], [math]\angle С_1В_1К_1=\angle СВК\Rightarrow К_1С_1=КС[/math]

Имеем, что [math]\angle(АВ_1;КВ)=\angle(АВ_1;К_1В_1)[/math]

Пусть а - длина ребра

Из [math]\bigtriangleup С_1К_1В_1[/math], [math]\angle С_1=90^\circ[/math], по теореме Пифагора : [math]К_1В_1=\sqrt{а^2+\frac{а^2}4}=\frac{а\sqrt5}2[/math]

Из [math]\bigtriangleup АК_1С_1[/math], [math]\angle С=90^\circ[/math], по теореме Пифагора : [math]АК_1=\sqrt{а^2+\frac{9а^2}4}=\frac{а\sqrt13}2[/math]

Из [math]\bigtriangleup АК_1С_1[/math]: [math]\angle В=90^\circ[/math] по теореме Пифагора: [math]АВ_1=\sqrt{а^2+а^2}=а\sqrt2[/math]

Проверим, является ли [math]\bigtriangleup АК_1В_1[/math] прямоугольным по теореме, обратной теореме Пифагора

[math]АК_1^2=АВ_1^2+К_1В_1^2[/math]

[math]\frac{а^2\cdot13}4=а^2\cdot2+\frac{а^2\cdot5}4[/math] - верно

Следовательно,[math]\bigtriangleup АВ_1К_1=90^\circ\Rightarrow\angle(АВ_1;К_1В_1)=\angle(АВ_1;КВ)\Rightarrow АВ_1\perp КВ[/math]

Б) Построим [math]С_1Н\perp А_1В_1[/math], [math]К_1H'\perp(AA_1B_1)[/math]

[math]C_1H\parallel K_1H'[/math] , [math]C_1K_1\parallel HH'\Rightarrow C_1H=K_1H'[/math]

Рассмотрим [math]\bigtriangleup С_1В_1H[/math] [math]\angle H=90^\circ[/math], [math]C_1H=\sqrt{C_1B_1^2-HB_1^2}[/math], по теореме Пифагора [math]HB_1=\frac12a[/math] ( по свойству равнобедренного треугольника)

[math]С_1Н=\sqrt{а^2-\frac{а^2}4}=\frac{а\sqrt3}2=К_1Н'[/math]

Рассмотрим пирамиду [math]K_1B_1BA[/math]:

С одной стороны [math]V_п=\frac13К_1Н'[/math] * [math]S_{\bigtriangleup ABB_1}[/math]

С другой стороны [math]V_п=\frac13h[/math] * [math]S_{\bigtriangleup AK_1B_1}[/math]

[math]\frac13К_1Н'[/math] * [math]S_{\bigtriangleup ABB_1}[/math] = [math]\frac13h\ast S_{\bigtriangleup AK_1B_1}\Rightarrow h=\frac{K_1H'\ast S_{\bigtriangleup ABB_1}}{S_{\bigtriangleup AK_1B_1}}[/math]

[math]S_{\bigtriangleup ABB_1}=\frac12a^2[/math], [math]S_{\bigtriangleup AK_1B_1}=\frac12\cdot\frac{a\sqrt5}2\cdot a\sqrt2[/math]

[math]h=\frac{\frac{a\sqrt3}2\cdot\frac{a^2}2}{\frac12\cdot\frac{a\sqrt5}2\cdot a\sqrt2}=a\frac{\sqrt3}{\sqrt{10}}=\frac{3\sqrt{30}}5[/math]

Ответ: [math]\frac{3\sqrt{30}}5[/math]