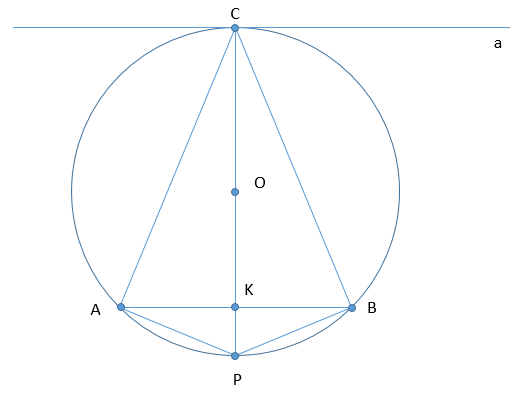
А) Пусть [math]a[/math] - касательная, данная по условию. [math]a\perp OC[/math] (по свойству касательной к окружности)[math]\Rightarrow a\perp CP[/math], [math]CP\cap AB=K[/math]

[math]a\perp CP;a\parallel AB\Rightarrow AB\perp CP[/math]

По свойству хорды, т.к. [math]AB\perp CP;AB[/math] - хорда [math]\Rightarrow AK=KB[/math]

т.к. [math]AK=KB;\angle AKB=\angle PKB=90^\circ;CK[/math] - общий [math]\Rightarrow\bigtriangleup ACK=\bigtriangleup CKB\Rightarrow AP=PB\Rightarrow\bigtriangleup APB[/math] - равнобедренный, ч.т.д.

Б) [math]\angle PBC=90^\circ[/math], т.к. вписанный и опирается на диаметр

Т.к. [math]\bigtriangleup APK=\bigtriangleup BPK[/math], [math]\angle APK=\angle BPK=\frac{150^\circ}2=75^\circ[/math]

[math]\angle PCB=180^\circ-75^\circ-90^\circ=15^\circ[/math]

[math]\bigtriangleup CKB[/math]: [math]CK=KB\cdot ctg15^\circ=KB\cdot ctg(45^\circ-30^\circ)=KB\cdot\frac{\sqrt3+1}{\sqrt3-1}[/math]

[math]\bigtriangleup PKB[/math]: [math]KP=KB\cdot ctg75^\circ[/math][math]KB\cdot tg15^\circ=KB\cdot\frac{\sqrt3-1}{\sqrt3+1}[/math]

[math]\frac{CK}{PK}=\frac{\left(\sqrt3+1\right)^2}{\left(\sqrt3-1\right)^2}=\frac{2+\sqrt3}{2-\sqrt3}[/math]

Ответ: [math]\frac{CK}{PK}=\frac{2+\sqrt3}{2-\sqrt3}[/math]