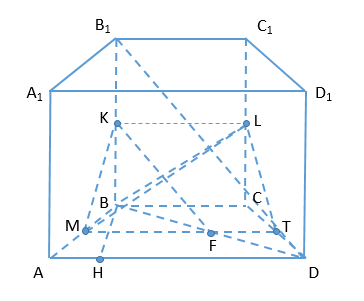
А) Пусть [math]M[/math] - середина [math]AB[/math]. Тогда [math]\alpha\cap(ABB_1)=MK[/math]

Проведем [math]B_1D;BD;KF\parallel B_1D[/math], тогда [math]\alpha\cap(ABC)=MT[/math], где [math]F\in MT[/math]. Точка [math]K[/math]-середина [math]BB_1[/math], [math]KF\parallel B_1D\Rightarrow F[/math] - середина [math]BD[/math] и [math]MF[/math] - средняя линия [math]\bigtriangleup ABD[/math][math]\Rightarrow MT\parallel AD\parallel BC[/math]. Тогда [math]MT\parallel(BCC_1)[/math] и [math]\alpha\cap(BCC_1)=KL\parallel BC[/math].

[math]\alpha\cap(DCC_1)=LT;MKTL=\alpha[/math] - сечение.

Имеем [math]KL\parallel BC\parallel MT;KL=BC\neq MT\Rightarrow MKLT[/math] - трапеция. А так как [math]\bigtriangleup MBK=\bigtriangleup TCL[/math] по двум катетам, то [math]MK=TL[/math] и [math]MKLT[/math] - равнобедренная трапеция.

Б) [math]V_{призмы}=S_{ABCD}\cdot AA_1[/math], [math]BH[/math] - высота [math]ABCD[/math]; [math]AH=\frac{25-7}2=9[/math], тогда [math]BH=12[/math], [math]S_{ABCD}=\frac{25+7}2\cdot12=192;V_{призмы}=192\cdot8=1536[/math]

Плоскость [math]\alpha[/math] разбивает призму на две части, меньшая из которых многогранник [math]MBKTCL[/math]. Плоскость [math]MBL[/math] разбивает этот многогранник на две пирамиды [math]LMBCT[/math] и [math]MBKL[/math], объемы которых обозначим [math]V_1[/math] и [math]V_2[/math] соответственно.

[math]V_1=\frac13S_{MBCT}\cdot CL;CL=4;MBCT[/math] - трапеция, высота которой [math]h=\frac{BH}2=6;MT=\frac{AD+BC}2=16[/math], тогда [math]V_1=\frac13\cdot\frac{7+16}2\cdot6\cdot4=92[/math]

[math]V_2=\frac13\cdot S_{BKL}\cdot\rho(M;(BKL));S_{BKL}=\frac12BK\cdot BC=\frac12\cdot7\cdot4=14[/math]

[math]AD\parallel(BKL);H\in AD\Rightarrow\rho(A;(BKL))=\rho(H;(BKL))=BH=12[/math]

[math]M[/math] - середина [math]AB[/math], тогда [math]\rho(M,(BKL))=\frac{\rho(A;(BKL))}2=\frac{BH}2=6[/math] и [math]V_2=\frac13\cdot14\cdot6=28[/math]

[math]V=V_{призмы}-(V_1+V_2)=1536-(92+28)=1416[/math]

Ответ: 1416