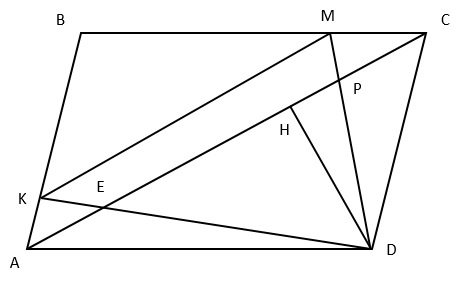
А) [math]\bigtriangleup AKE\sim\bigtriangleup DCE[/math] (по двум углам): [math]\angle KEA=\angle DEC[/math] - вертикальные, [math]\angle KАЕ=\angle DСЕ[/math] - накрест лежащие при [math]AB\parallel CD[/math]

[math]\Rightarrow\frac{AK}{CD}=\frac{AE}{EC}=\frac13[/math], [math]\frac{AK}{AB}=\frac13[/math]

[math]\frac{BA-BK}{AB}=\frac13\Rightarrow\frac{BK}{AB}=\frac23[/math]

[math]\bigtriangleup CMP\sim\bigtriangleup ADP[/math] ( по двум углам): [math]\angle MPC=\angle DPA[/math] - вертикальные, [math]\angle MCP=\angle DAP[/math] - накрест лежащие при [math]BC\parallel AD[/math]

[math]\Rightarrow\frac{MC}{AD}=\frac{CP}{AP}=\frac13[/math], [math]\frac{MC}{BC}=\frac13[/math] [math]\Rightarrow\frac{BM}{BC}=\frac23[/math]

[math]\frac{BK}{AB}=\frac23[/math], [math]\frac{BM}{BC}=\frac23[/math], [math]\angle B[/math] - общий[math]\Rightarrow\bigtriangleup KBM\sim\bigtriangleup ABC[/math] (по двум пропорциональным сторонам и углу между ними)[math]\Rightarrow\angle BMK=\angle BCA[/math], [math]\angle BKM=\angle BAC\Rightarrow KM\parallel AC[/math], ч.т.д.

Б) [math]S_{ABCD}=2(S_{AKEPM}+S_{AEK}+S_{CPM})[/math]

Из точки D опустим перпендикуляр DH на AC

[math]S_{\bigtriangleup ACD}=\frac12S_{ABCD=}\frac12AC\cdot DH[/math], [math]S_{\bigtriangleup ECD}=\frac12EC\cdot DH=\frac34S_{\bigtriangleup ACD}=\frac38S_{ABCD}[/math], [math]S_{\bigtriangleup APD}=\frac12AP\cdot DH=\frac34S_{\bigtriangleup ACD}=\frac38S_{ABCD}[/math]

[math]\Rightarrow[/math] (смотрите п.А) [math]S_{\bigtriangleup AKE}=\frac19S_{\bigtriangleup ECD}=\frac3{72}S_{ABCD}[/math], [math]S_{\bigtriangleup CMP}=\frac19S_{\bigtriangleup APD}=\frac3{72}S_{ABCD}[/math]

Тогда [math]S_{ABCD}=2S_{BKEPM}+\frac6{72}S_{ABCD}+\frac6{72}S_{ABCD}\Rightarrow S_{ABCD}=72[/math]

Ответ: 72