А) [math]sinx\cdot cos4x=1[/math]

[math]sin2x(1-2sin^2x)=1[/math]

[math]-2sin^3(2x)+sin2x-1=0[/math]

[math](sin2x+1)(-2sin^2(2x)+2sin2x-1)=0[/math]

Имеем, что [math]-2sin^2(2x)+2sin2x-1=0[/math] или [math]sin2x+1=0[/math]

[math]-2sin^2x+2sin2x-1=0[/math]

[math]D=4-8<0[/math] корней нет

[math]sin2x+1=0[/math]

[math]sin2x=-1[/math]

[math]2x=-\frac\pi2+2\pi n[/math], [math]n\in Z[/math]

[math]x=-\frac\pi4+\pi n[/math], [math]n\in Z[/math]

Б) Нанесем корни на числовую прямую и определим,какие из них попадают в промежуток

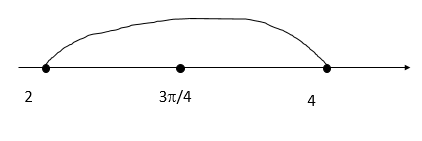
Ответ: а) [math]-\frac\pi4+\pi n,\;n\in Z[/math]

б) [math]\frac{3\pi}4[/math]