Вариант 9
Математика Профильный уровень
Часть 1
Ответом на задания 1—12 должно быть целое число или десятичная дробь.
На изготовление шкатулки на уроке труда требуется 3,5 листа картона. В пачке картона 10 листов. Сколько потребуется пачек картона для изготовления шкатулок классу из 23 человек?
На диаграмме изображена средняя влажность воздуха за июнь 2014 года в различных городах. По горизонтали представлена средняя влажность воздуха в %, по вертикали — названия городов.
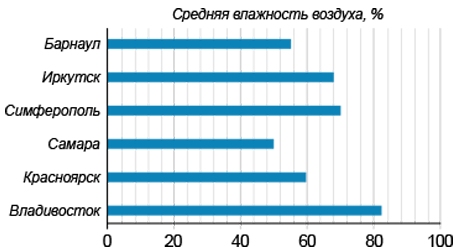
Определите по диаграмме, в скольких городах из представленных средняя влажность воздуха в июне превышала 60 %.
На клетчатой бумаге с размером клетки 1 см × 1 см изображён многоугольник. Найдите его площадь. Ответ дайте в см2
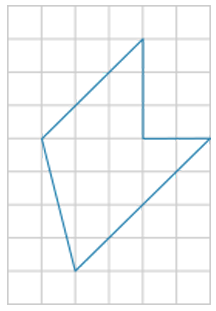
Билет моментальной лотереи оказывается выигрышным с вероятностью 0,4. Маша купила 3 билета. Какова вероятность того, что 2 билета окажутся выигрышными, а третий нет?
Решите уравнение [math]\left(\frac2{54}\right)^{2x-5}=3^{18}[/math]
К окружности проведены касательная AD=9 см и секущая AC, проходящая через центр окружности точку O. Найдите площадь треугольника AOD (в см2, если диаметр окружности BC=8 см.
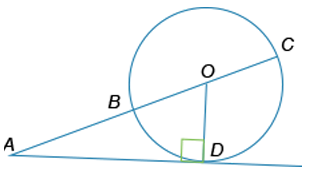
На рисунке изображён график функции f(x). Укажите количество точек, в которых производная функции равна нулю.
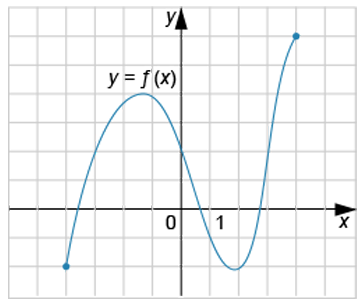
В цилиндр вписан конус. Объём конуса равен [math]196\pi[/math]см3, а высота —12 см. Найдите площадь боковой поверхности цилиндра в см2. В ответе укажите площадь, делённую на [math]\pi[/math].
Найдите значение выражения [math]\frac{\left(n^5\right)^{-6}}{\left(2m^3\right)^2}\div\frac{\left(n^{-10}\right)^3}{m^6}[/math]
Кинетическую энергию (в Дж) тела можно рассчитать по формуле [math]E_k=\frac{mv^2}2[/math], где m — масса тела (в кг), v — скорость тела (в м/с). Какова масса тела в (кг.), если при скорости 120 м/с оно приобретает энергию 36 000 Дж?
К 25-процентному раствору щелочи добавили 40-процентный и получили 37,5-процентный раствор. Если к данной смеси добавить 6 литров воды, то получится 30-процентный раствор. Найдите объём 40-процентного раствора (в л).
Найдите наименьшее значение функции [math]y=x^3+4,5x^2-12x+17[/math] на промежутке [0;7].
Часть 2.
При выполнении заданий 13—19 требуется записать полное решение и ответ.
Дано уравнение sin2x ⋅ cos4x=1.
А) Решите уравнение.
Б) Найдите его корни, принадлежащие отрезку [2; 4].
А) [math]sinx\cdot cos4x=1[/math]
[math]sin2x(1-2sin^2x)=1[/math]
[math]-2sin^3(2x)+sin2x-1=0[/math]
[math](sin2x+1)(-2sin^2(2x)+2sin2x-1)=0[/math]
Имеем, что [math]-2sin^2(2x)+2sin2x-1=0[/math] или [math]sin2x+1=0[/math]
[math]-2sin^2x+2sin2x-1=0[/math]
[math]D=4-8<0[/math] корней нет
[math]sin2x+1=0[/math]
[math]sin2x=-1[/math]
[math]2x=-\frac\pi2+2\pi n[/math], [math]n\in Z[/math]
[math]x=-\frac\pi4+\pi n[/math], [math]n\in Z[/math]
Б) Нанесем корни на числовую прямую и определим,какие из них попадают в промежуток
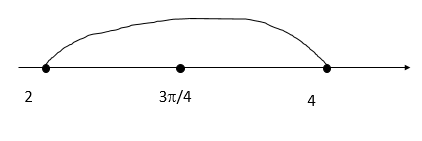
Ответ: а) [math]-\frac\pi4+\pi n,\;n\in Z[/math]
б) [math]\frac{3\pi}4[/math]
В правильной пирамиде PABC точки Е, F, K, M, N - середины ребер АС, ВС, РА, РВ и РС соответственно.
А) Докажите, что объем пирамиды NEFMK составляет четверть объема пирамиды PABC.
Б) Найдите радиус сферы, проходящей через точки N, Е, F, M, K, если известно, что АВ=8, АР=6.

А) Доказать, что [math]V_{NEFMK}=\frac14V_{PABC}[/math]
Обозначим за длину ребра основания [math]a[/math], а за длину ребра боковой грани - [math]b[/math].
[math]V_{PABC}=\frac13S_{\bigtriangleup ABC}\cdot PO[/math], где [math]PO[/math] - высота пирамиды.
[math]S_{\bigtriangleup ABC}=\frac12AC\cdot BE[/math], где [math]BE[/math] - высота треугольника, и его биссектриса (т.к. [math]\bigtriangleup ABC[/math] - равносторонний) [math]\Rightarrow O\in BE[/math]
Из [math]\bigtriangleup BEC[/math], по теореме Пифагора: [math]BE=\sqrt{BC^2-EC^2}=\sqrt{a^2-\frac14a^2}=\frac{\sqrt3}2a\Rightarrow S_{\bigtriangleup ABC}=\frac12a\cdot\frac{\sqrt3}2a=\frac{\sqrt3}4a^2[/math]
т.к.[math]\bigtriangleup ABC[/math] - равносторонний, то т.О - точка пересечения медиан и [math]\frac{OB}{OE}=\frac21[/math] или [math]OB=\frac23EB=\frac{\sqrt3}3a[/math]
Рассмотрим [math]\bigtriangleup POB[/math], по теореме Пифагора: [math]PB=\sqrt{OB^2+OP^2}\Rightarrow PO=\sqrt{PB^2-OB^2}=\sqrt{b^2-\frac13a^2}[/math]
[math]\Rightarrow V_{PABC}=\frac13\cdot\frac{\sqrt3}4a^2\sqrt{b^2-\frac13a^2}=\frac{\sqrt3}{12}a^2\sqrt{b^2-\frac13a^2}[/math]
В [math]\bigtriangleup APC[/math] [math]EK[/math] - средняя линия [math]\Rightarrow EK=\frac12b;EK\parallel PC[/math]
В [math]\bigtriangleup BPC[/math] [math]MF[/math] - средняя линия [math]\Rightarrow MF=\frac12b;MF\parallel PC[/math]
В [math]\bigtriangleup CAB[/math] [math]EF[/math] - средняя линия [math]\Rightarrow EF=\frac12b;EF\parallel AB[/math]
В [math]\bigtriangleup PAB[/math] [math]KM[/math] - средняя линия [math]\Rightarrow KM=\frac12b;KM\parallel AB[/math]
[math]CS\perp AB[/math],[math]CS[/math] - проекция [math]CP[/math] [math]\Rightarrow CP\perp AB[/math] (по теореме о трех перпендикулярах)
[math]\Rightarrow KM\perp MF[/math] и [math]KMFE[/math] - прямоугольник, [math]S_{KMFE}=KM\cdot MF=\frac14ab[/math]
Выполним чертеж пирамиды [math]NKMFE[/math]

Построим [math]XY\parallel KE\parallel MF[/math], так, что [math]H\in XY[/math] [math]XY=MF=KE=\frac b2[/math]
При этом, [math]NY\perp EF;NX\perp MK\Rightarrow[/math] по теореме о трех перпендикулярах
и [math]EY=YF[/math], т.е. [math]\bigtriangleup PEF[/math] - равнобедренный, [math]KX=MX[/math], т.к. [math]\bigtriangleup PMK[/math] - равнобедренный (равносторонний) [math]EY=YF=KX=MX=\frac a4[/math]
Из [math]\bigtriangleup NYE[/math], по теореме Пифагора [math]NY=\sqrt{\frac14b^2-\frac16a^2}[/math]
Из [math]\bigtriangleup NXK[/math], по теореме Пифагора [math]NX=\sqrt{\frac14a^2-\frac16a^2}=\frac{\sqrt3}4a[/math]
Рассмотрим теорему косинусов для [math]\bigtriangleup NXY[/math]:
[math]NX^2=NY^2+XY^2-2NY\cdot XY\cdot cos(\angle NYX)[/math]
[math]NY^2=NX^2+XY^2-2NX\cdot XY\cdot cos(\angle NXY)[/math]
[math]\frac14b^2-\frac1{16}a^2=\frac3{16}a^2+\frac{b^2}4-2\cdot\frac{\sqrt3}4a\cdot\frac b2\cdot cos(\angle PXY)[/math]
[math]\frac{\sqrt3ab}4\cdot cos(\angle NXY)=\frac14a^2\Rightarrow cos(\angle NXY)=\frac a{\sqrt3b}[/math]
[math]NH=NX\cdot sin(\angle NXY)=\frac{\sqrt3}4a\cdot\sqrt{1-\frac{a^2}{3b^2}}=\frac{\sqrt3}4\cdot\frac ab\cdot\sqrt{b^2-\frac{a^2}3}[/math]
[math]V_{NKMFE}=\frac13S_{KMFE}\cdot NH=\frac13\cdot\frac14ab\cdot\frac{\sqrt3}4\cdot\frac ab\sqrt{b^2-\frac{a^2}3}=\frac{\sqrt3}{48}a^2\sqrt{b^2-\frac13a^2}\Rightarrow\frac{V_{NKMFE}}{V_{PABC}}=\frac14[/math], [math]V_{NKMFE}=\frac14V_{PABC}[/math], чтд
Б) Поставим т.Z - точка пересечения диагоналей прямоугольника [math]KMFE[/math]
[math]MZ=ZF=ZE=ZK=\frac12ME[/math] ([math]ME[/math] из [math]\bigtriangleup MEF[/math]: [math]ME=\sqrt{MF^2+ME^2}=\sqrt{9+16}=5[/math]
[math]MZ=ZF=ZE=ZK=2.5[/math]
Рассмотрим [math]\bigtriangleup MNE[/math], [math]NE=3;NM=4;ME=5[/math]. Проверим обратную теорему Пифагора: [math]ME^2=NM^2+NE^2:25=9+16[/math] - верно, значит [math]\angle MNE=90^\circ[/math] и [math]NZ=\frac12ME[/math] (как медиана прямоугольного треугольника)
[math]NZ=2,5=MZ=ZF=ZE=ZK\Rightarrow Z[/math] - центр отсеченной сферы и [math]R=NZ=2.5[/math]
Ответ: 2,5
Решите неравенство |3x+1 — 9x| + |9x — 5 ⋅ 3x+6| ≤ 6 — 2 ⋅ 3x.
Применим свойства модулей, а именно следующие: [math]\left|a+b\right|\leq\left|a\right|+\left|b\right|;a\leq\left|a\right|[/math]
Получим [math]6-2\cdot3^x\geq\left|3^{x+1}-3^{2x}\right|+\left|3^{2x}-5\cdot3^x+6\right|\geq\left|3^{x+1}-3^{2x}+3^{2x}-5\cdot3^x+6\right|[/math]
[math]6-2\cdot3^x\leq\left|6-2\cdot3^x\right|[/math]
Из этого следует, что [math]\left|3^{x+1}-3^{2x}\right|+\left|3^{2x}-5\cdot3^x+6\right|=\left|6-2\cdot3^x\right|[/math]
Так же мы выяснили, что [math]3^{x+1}-3^{2x}+3^{2x}-5\cdot3^x+6=6-2\cdot3^x[/math]
Значит имеем два случая.
1 сл:[math]3^{x+1}-3^{2x}\geq0\;;3^{2x}-5\cdot3^x+6\geq0[/math]
[math]3^{x+1}-3^{2x}\geq0\;[/math] Нули: [math]3^x=3\Rightarrow x=1[/math]
[math]3^{2x}-5\cdot3^x+6\geq0[/math] Нули:[math]3^x=2\Rightarrow x=log_32;3^x=3\Rightarrow x=1[/math]
Нанесем на числовую прямую и расставим знаки:
4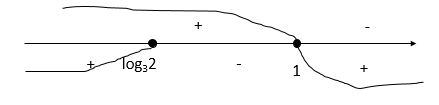
2 сл: [math]3^{x+1}-3^{2x}\leq0\;;3^{2x}-5\cdot3^x+6\leq0[/math]
[math]3^{x+1}-3^{2x}\leq0\;[/math] Нули: [math]3^x=3\Rightarrow x=1[/math]
[math]3^{2x}-5\cdot3^x+6\leq0[/math] Нули:[math]3^x=2\Rightarrow x=log_32;3^x=3\Rightarrow x=1[/math]
Нанесем на числовую прямую и расставим знаки:
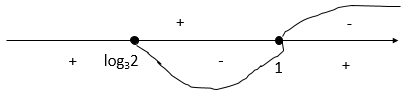
Общее решение: (-∞; log32)⋃{1}
Ответ: (-∞; log32)⋃{1}
Дан квадрат ABCD. Точки К, L, M - середины сторон АВ, ВС и CD соответственно. AL пересекает DK в точке Р; DL пересекает АМ в точке Т; АМ пересекает DK в точке О.
А) Докажите, что точки Р, L, T, O лежат на одной окружности;
Б) Найдите радиус окружности, вписанной в четырехугольник PLTO, если АВ=4.

А) Доказать, что точки Р, L, T, O лежат на одной окружности. Таким образом, нужно доказать, что вокруг POTL можно описать окружность, это возможно, если [math]\angle POT+\angle TLP=180^\circ[/math], [math]\angle OTL+\angle OPL=180^\circ[/math]
Рассмотрим [math]\bigtriangleup AOD[/math]:
[math]tg(\angle DAO)=\frac{DM}{AD}=\frac12[/math] (из [math]\bigtriangleup DAM[/math] )
[math]tg(\angle ADO)=\frac{AK}{AD}=\frac12[/math] (из [math]\bigtriangleup DAK[/math] )
[math]\Rightarrow\angle AOD=180^\circ-2arctg(\frac12)=\angle POT[/math] (как вертикальные)
В [math]\bigtriangleup LDC[/math]: [math]\angle C=90^\circ[/math], [math]tg(\angle LDC)=\frac{LC}{DC}=\frac12\Rightarrow\angle DLC=90-arctg(\frac12)[/math]
В [math]\bigtriangleup LAB[/math]: [math]\angle B=90^\circ[/math], [math]tg(\angle LAB)=\frac{LB}{AB}=\frac12\Rightarrow\angle ALB=90-arctg(\frac12)[/math]
[math]\Rightarrow\angle ALD=180^\circ-(90^\circ-arctg(\frac12))-(90^\circ-arctg(\frac12))=2arctg(\frac12)[/math] (как смежный с [math]\angle DLC[/math] и [math]\angle ALB[/math])
Тогда [math]\angle POT+\angle TLP=180^\circ-2arctg(\frac12)+2arctg(\frac12)=180^\circ[/math] и [math]\angle OTL+\angle OPL=360^\circ-(\angle POT+\angle TLP)=180^\circ[/math] (по свойству четырехугольника) . Следовательно, точки Р, L, T, O лежат на одной окружности, что и требовалось доказать.
Б) AB=4, r-?
Окружность с центром в т.Н вписана в POTL, следовательно окружность с центром в т.Н вписана в [math]\bigtriangleup DPL[/math]. Имеем, что задача сведена к поиску радиуса вписанной в [math]\bigtriangleup DPL[/math] окружности.
Из [math]\bigtriangleup DLC[/math] по теореме Пифагора: [math]DL=\sqrt{DC^2+LC^2}[/math] [math]DL=\sqrt{16+4}=2\sqrt5[/math]
Аналогично: [math]AL=DL=DK=AM=2\sqrt5[/math]
Ранее доказывалось, что [math]\angle LDC=\angle BAL=\angle KDA=arctg(\frac12)[/math] и [math]\angle DLC=90-arctg(\frac12)[/math]
[math]\Rightarrow\angle DKA=90-\angle KDA=90-arctg(\frac12)[/math]
Получаем, что [math]\bigtriangleup PAK\sim\angle CDL[/math] (по двум углам: [math]\angle LDC=\angle KAP;\angle CLD=\angle PKA[/math]) и [math]\frac{DL}{AK}=\frac{DC}{AP}=\frac{CL}{PK}\Rightarrow\frac{2\sqrt5}2=\frac4{AP}=\frac2{PK}\Rightarrow AP=\frac4{\sqrt5}=\frac{4\sqrt5}5;PK=\frac2{\sqrt5}=\frac{2\sqrt5}5[/math]
Причем [math]\angle KPA=\angle C=90^\circ[/math] и [math]\angle DPL=\angle KPA=90^\circ[/math] (как вертикальные)
[math]PL=AL-AP=2\sqrt5-\frac{4\sqrt5}5=\frac{6\sqrt5}5[/math]
[math]DP=DK-PK=2\sqrt5-\frac{2\sqrt5}5=\frac{8\sqrt5}5[/math]
Тогда [math]r=\frac{PL+DP-DL}2[/math] (формула для радиуса вписанной в прямоугольный треугольник окружности)
[math]r=\frac{\frac{6\sqrt5}5+\frac{8\sqrt5}5-2\sqrt5}2=\frac{3\sqrt5}5+\frac{4\sqrt5}5-\sqrt5=\frac{7\sqrt5}5-\frac{5\sqrt5}5=\frac{2\sqrt5}5[/math]
Ответ: [math]\frac{2\sqrt5}5[/math]
Два пешехода идут навстречу друг другу: один из А в В, а другой - из В в А. Они вышли одновременно, и когда первый прошел половину пути, второму оставалось идти еще 1,5 часа, а когда второй прошел половину пути, то первому оставалось идти еще 45 минут. На сколько минут раньше закончит свой путь первый пешеход, чем второй?
Пусть первый пешеход прошел путь за x часов, а второй- за у часов.
Из условия задачи имеем, что половина пути составила для первого половину его времени, а именно [math]1/2 х= у-90[/math], аналогично со вторым[math]1/2 у= х-45[/math]. Решим уравнения и найдем значения x и y:
[math]х= 2у-180;у= 2х-90[/math]
[math] у= 2(2у-180)-90[/math]
[math]4у-360-90-у=0[/math].
Решение: у= 150 (минут). х= 2*150-180= 120 (мин)
Разница составляет 150-120=30 минут.
Ответ: 30
Найдите все значения параметра а, при каждом из которых уравнение [math]\log_2^2\left|4-x^2\right|-2a\cdot\log_2\left|x^2-4\right|+a+6=0[/math] имеет ровно четыре различных корня.
[math]\left(log_2\left|x^2-4\right|\right)^2-2alog_2\left|x^2-4\right|+a+6=0[/math]
Перед нами квадратное уравнение относительно [math]log_2\left|x^2-4\right|[/math]
Найдем дискриминант [math]D=4a^2-4(a+6)=4a^2-4a-24[/math]
Уравнение не имеет решение, если [math]4a^2-4a-24<0[/math]
Нули: [math]a=-2;a=3[/math]
Нанесем на числовую прямую и определим знаки:
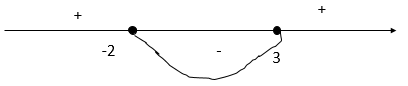
Значит при [math]a\in(-2;3)[/math] уравнение не имеет решений.
Рассмотрим случай, когда [math]a\not\in(-2;3)[/math]
Найдем корни: [math]log_2\left|x^2-4\right|=a\pm\sqrt{a^2-a-6}[/math]
[math]\left|x^2-4\right|=2^{a\pm\sqrt{a^2-a-6}}[/math]
[math]x^2=4\pm2^{a\pm\sqrt{a^2-a-6}}[/math]
Определим количество корней на концах промежутка:
[math]a=-2[/math] [math]x^2=\frac54;x^2=\frac{15}4[/math] - четыре корня, входит в ответ
[math]a=3;x^2=12;x^2=-4[/math] - два корня, не входит в ответ
В остальных случаях [math]x^2=4\pm2^{a\pm\sqrt{a^2-a-6}}[/math]
Значит, необходимо чтобы два из них не подходили под условие, что [math]x^2>0[/math]
т.е имеем, что [math]4-2^{a\pm\sqrt{a^2-a-6}}<0[/math]
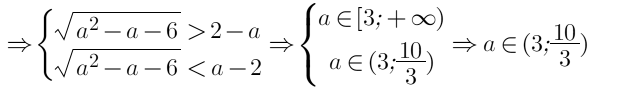
Ответ: [math]\left\{-2\right\}\cup\left(3;\;\frac{10}3\right)[/math]
Про натуральное пятизначное число N известно, что оно делится на 12, и сумма его цифр делится на 12.
A) Могут ли все пять цифр в записи числа N быть различными?
Б) Найдите наименьшее возможное число N;
B) Найдите наибольшее возможное число N;
Г) Какое наибольшее количество одинаковых цифр может содержаться в записи числа N? Сколько всего таких чисел N (содержащих в своей записи наибольшее количество одинаковых цифр)?
Примем во внимание , что :
1. Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.
2. Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.
3. Число делится на 4 тогда и только тогда, когда число из двух последних его цифр нули или делится на 4.
Для удобства примем пятизначное число в виде abcde.Имеем, что abcde делится на 12, a+b+c+d+e делится на 3 и на 12, de делится на 4
А) Если a+b+c+d+e делится на 12, то имеем три варианта: a+b+c+d+e=12;24;36 (9*5=45, больше сорока сумма не может быть). Проще рассмотреть сразу вариант 12, т.к. при 24 и 36 скорее всего цифры будут повторяться,т.к. они достаточно большие
Вариант 0+1+2+3+4=10, чтобы было 12, достаточно исправить одну цифру 0+1+2+3+6=12, имеем, что 36 делится на 4, 0+1+2+3+6 делится на 3 и на 12, т.е. все условия удовлетворены. Имеем число 10236, что означает существование числа с различными цифрами
Б) Если a+b+c+d+e делится на 12, то имеем три варианта: a+b+c+d+e=12;24;36 (9*5=45, больше сорока сумма не может быть). Чтобы получить наименьшее число, необходимо учитывать, что на старших разрядах должны быть наименьшие цифры, т.е. 1 на первом место-хороший вариант. Получим наилучший набор цифр 1,0,0,5,6, проверим все условия: 56 делится на 4, 1+0+5+6=12 делится на 12. Остальной набор цифр давал бы вместо нулей другие цифры, что явно давало бы больше число, а сочетания дающие в двух последних цифрах сумму, равную 11, т.е 2 и 9, 3 и 8, 4 и 7 не дают число, делящееся на 4
В) Если a+b+c+d+e делится на 12, то имеем три варианта: a+b+c+d+e=12;24;36 (9*5=45, больше сорока сумма не может быть). Чтобы получить наименьшее число, необходимо учитывать, что на старших разрядах должны быть наибольшие цифры, т.е. 9 на первом место-хороший вариант.И сумма цифр будет 36
Берем максимальное количество 9 и 2 последние цифры, дающие число, делящееся на 4,при том сумма должна делиться на 3 т.е. 9,9,9 и варианты: 36-3*9=9, 9 в сумме дают числа 1 и 8,2 и 7,3 и 6, 4 и 5( Условию подходит 72,36, 72-наибольшее). Имеем число 99972
Г) Если a+b+c+d+e делится на 12, то имеем три варианта: a+b+c+d+e=12;24;36 (9*5=45, больше сорока сумма не может быть). Пять одинаковых цифр не может быть. Возьмем за основу два момента: 4 одинаковых цифр и число из двух последних делится на 4.Имеем следующие варианты (не учитывая порядок цифр):
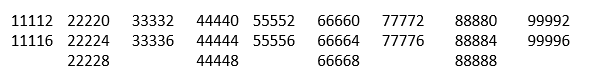
Из них исключаем те, сумма цифр которых не равна 12,24 или 36.Получим( учитывая порядок цифр):

а) да, например,10236, 12504; б) 10056; в) 99972; г) 4; 12 чисел.
| № | Ваш ответ | Ответ и решение | Первичный балл |
|---|---|---|---|
|
Здесь появится результат первой части. Нажмите на кнопку «Завершить работу», чтобы увидеть правильные ответы и посмотреть решения. |
|||