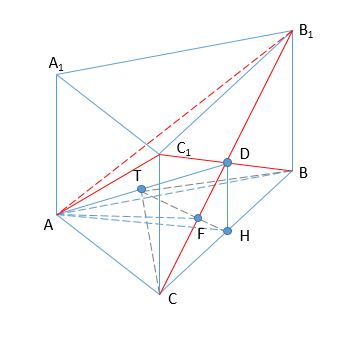
А) Доказать, что прямая В₁С₁ перпендикулярна линии пересечения плоскостей АВС₁ и АСВ₁.

т. [math]A\in(ABC_1)[/math]. т. [math]A\in(ACB_1)[/math]

[math]C_1B\in(ABC_1)[/math], [math]B_1C\in(ACB_1)[/math]

[math]C_1B\cap CB_1=D\Rightarrow D\in(ABC_1);D\in(ACB_1)[/math]

и [math]AD\in(ABC_1);AD\in(ACB_1)\Rightarrow AD[/math] - линия пересечения [math](ABC_1)[/math] и [math](ACB_1)[/math]

Имеем: необходимо доказать [math]B_1C_1\perp AD[/math]

Опустим из D перпендикуляр DH на CB ([math]DH\perp CB[/math])

т.D - не только высота треугольника, но и медиана,т.е.[math]CH=HB[/math]

т.к. [math]\bigtriangleup ABC[/math] - правильный, то AH - не только медиана, но и высота [math]\Rightarrow AH\perp CB[/math]

Тогда [math]AD\perp CB[/math] (по теореме о трех перпендикулярах)

А т.к. [math]CB\parallel C_1B_1[/math], то [math]AD\perp C_1B_1[/math], что и требовалось доказать

Б) [math]AB=2;AA_1=2;\angle((ABC_1);(ACB_1)-?[/math]

Опустим из C и B перпендикуляры на AD. Исходя из равенства [math]\bigtriangleup ADC=\bigtriangleup ADB[/math] (по трем сторонам) они упадут на одну точку, пусть т.Т

Имеем [math]CT\perp AD,BT\perp AD[/math], [math]\angle CTB[/math] - линейный угол искомого двугранного угла

[math]\bigtriangleup CTB[/math] - равносторонний [math]\Rightarrow TH\perp CB[/math]

Тогда [math]sin(\frac12\angle CTB)=\frac{HC}{CT}[/math]

Из [math]\bigtriangleup CHD[/math] по теореме Пифагора: [math]CD=\sqrt{CH^2+HD^2}[/math] ([math]HD=\frac12BB_1[/math]) [math]CD=\sqrt{1+1}=\sqrt2[/math]

Из [math]\bigtriangleup CHA[/math] по теореме Пифагора: [math]AH=\sqrt{AC^2-CH^2}[/math] [math]AH=\sqrt{4-1}=\sqrt3[/math]

Из [math]\bigtriangleup AHD[/math] по теореме Пифагора: [math]AD=\sqrt{AH^2+HD^2}[/math] [math]AH=\sqrt{3+1}=2[/math]

Имеем [math]AC=AD\Rightarrow\bigtriangleup CAD[/math] - равнобедренный . Опустим из А [math]AF\perp CD[/math]

При этом [math]CF=FD=\frac12CD=\frac{\sqrt2}2[/math]

Тогда из [math]\bigtriangleup AFC[/math] по теореме Пифагора [math]AF=\sqrt{AC^2-CF^2}=\sqrt{4-\frac12}=\sqrt{\frac72}[/math]

С одной стороны, [math]S_{\bigtriangleup ADC}=\frac12CT\cdot AD[/math], с другой стороны[math]S_{\bigtriangleup ADC}=\frac12AF\cdot CD\Rightarrow CT\cdot AD=AF\cdot CD\Rightarrow2CT=\sqrt{\frac72}\cdot\sqrt2\Rightarrow CT=\frac{\sqrt7}2[/math]

[math]sin(\frac12\angle CTB)=\frac1{\frac{\sqrt7}2}=\frac2{\sqrt7}\Rightarrow cos(\frac12\angle CTB)=\sqrt{1-\frac47}=\sqrt{\frac37}[/math], [math]sin(\angle((ABC_1);(ACB_1)))=2\cdot\frac2{\sqrt7}\cdot\sqrt{\frac37}=\frac{4\sqrt3}7[/math] и [math]cos(\angle((ABC_1);(ACB_1)))=\sqrt{1-\frac{16\cdot3}{49}}=\frac17[/math]

[math]\Rightarrow\angle((ABC_1);(ACB_1))=arccos(\frac17)[/math]

Ответ: [math]arccos\frac17[/math]